18 Ordered Logistic Regression - Ex: Spaking

18.1 PREPARATION

18.1.1 Load Packages

# install.packages("remotes")
# remotes::install_github("sarbearschwartz/apaSupp") # 9/17/2025

library(haven)
library(tidyverse)   
library(flextable)
library(apaSupp)       # not on CRAN, get from GitHub (above) 
library(car)          
library(car)          
library(MASS)         
library(nnet)         
library(pscl)

18.1.2 Background

This dataset comes from John Hoffman’s textbook: Regression Models for Categorical, Count, and Related Variables: An Applied Approach (2004) Amazon link, 2014 edition

Chapter 4: Ordered Logistic and Probit Regression Models

Dataset: The following example uses the SPSS data set gss.sav. The dependent variable of interest is labeled spanking.

” The pertinent question (spanking) asks “Do you strongly agree, agree, disagree, or strongly disagree that it is sometimes necessary to discipline a child with a good, hard spanking?” The possible answers are coded as 1 = strongly agree, 2 = agree, 3 = disagree, and 4 = strongly disagree. A common hypothesis is that support for corporal punishment of children decreases at higher levels of education.”

18.1.3 Raw Dataset

df_gss <- haven::read_spss("https://raw.githubusercontent.com/CEHS-research/data/master/Hoffmann_datasets/gss.sav") %>% 
  haven::as_factor() %>% 
  haven::zap_formats() %>% 
  haven::zap_label() %>% 
  haven::zap_widths() %>% 
  dplyr::mutate_if(is.factor, ~forcats::fct_relabel(.x, stringr::str_to_title)) %>% 
  dplyr::mutate(spankingN = as.numeric(spanking)) %>%   # numeric version: 1, 2, 3, 4
  dplyr::mutate(polviewsN = as.numeric(polviews)) %>% 
  dplyr::mutate(educateF = as.factor(educate))
str(df_gss)
tibble [2,903 × 23] (S3: tbl_df/tbl/data.frame)
 $ id       : num [1:2903] 402 1473 1909 334 1751 ...
 $ marital  : Factor w/ 5 levels "Married","Widowed",..: 3 2 2 2 1 3 5 1 5 2 ...
 $ divorce  : Factor w/ 2 levels "Yes","No": 1 2 2 1 2 1 2 1 2 2 ...
 $ childs   : Factor w/ 9 levels "0","1","2","3",..: 3 1 8 3 3 1 3 4 1 3 ...
 $ age      : num [1:2903] 54 24 75 41 37 40 36 33 18 35 ...
 $ income   : num [1:2903] 10 2 NA NA 12 NA 9 NA NA 6 ...
 $ polviews : Factor w/ 7 levels "Extreme Liberal",..: 4 5 7 4 7 7 NA 4 4 4 ...
 $ fund     : Factor w/ 3 levels "Fundamentalist",..: NA NA NA NA NA NA NA NA NA NA ...
 $ attend   : Factor w/ 9 levels "Never","Less Than Once A Year",..: NA NA NA NA NA NA 7 4 3 4 ...
 $ spanking : Factor w/ 4 levels "Strongly Agree",..: NA NA NA NA NA NA NA NA NA NA ...
 $ totrelig : num [1:2903] NA NA NA NA NA NA NA 1000 NA NA ...
 $ sei      : num [1:2903] 38.9 29 29.1 29 38.1 ...
 $ pasei    : num [1:2903] NA 48.6 22.5 26.7 38.1 ...
 $ volteer  : num [1:2903] 0 0 0 1 1 0 0 0 1 0 ...
 $ female   : Factor w/ 2 levels "Male","Female": 2 1 2 2 1 2 2 2 2 1 ...
 $ nonwhite : Factor w/ 2 levels "White","Non-White": 2 1 2 1 1 1 2 1 2 1 ...
 $ prayer   : Factor w/ 6 levels "Never","Less Than Once A Week",..: 5 4 5 4 4 4 5 4 4 4 ...
 $ educate  : num [1:2903] 12 17 8 12 12 NA 15 12 11 14 ...
 $ volrelig : Factor w/ 2 levels "No","Yes": 1 1 1 2 2 1 1 1 1 1 ...
 $ polview1 : Factor w/ 3 levels "Liberal","Moderate",..: 2 3 3 2 3 3 NA 2 2 2 ...
 $ spankingN: num [1:2903] NA NA NA NA NA NA NA NA NA NA ...
 $ polviewsN: num [1:2903] 4 5 7 4 7 7 NA 4 4 4 ...
 $ educateF : Factor w/ 19 levels "0","3","4","5",..: 11 16 7 11 11 NA 14 11 10 13 ...

18.1.4 Wrangle Data

df_gss_model <- df_gss %>% 
  dplyr::filter(complete.cases(educate, spanking))      # only include complete cases
df_gss_model %>% 
  dplyr::select("spanking_num" = spankingN, 
                "spanking_fct" = spanking, 
                female, 
                nonwhite, 
                "educate_num" = educate, 
                "educate_fct" = educateF,
                income,
                "polviews_num" = polviewsN, 
                "polviews_fct" = polviews) %>% 
  psych::headTail() %>% 
  flextable::flextable() %>% 
  flextable::separate_header() %>% 
  apaSupp::theme_apa(caption = "View Data") %>% 
  flextable::hline(part = "header", i = 1)
Table 18.1
View Data

spanking

female

nonwhite

educate

income

polviews

num

fct

num

fct

num

fct

2

Agree

Male

White

16

16

12

6

Conservative

2

Agree

Female

White

11

11

2

5

Slight Conservative

3

Disagree

Male

White

15

15

12

7

Extreme Conservative

3

Disagree

Male

White

14

14

4

Middle Of The Road

...

...

...

...

4

Strongly Disagree

Female

Non-White

16

16

12

2

Liberal

2

Agree

Female

Non-White

14

14

12

5

Slight Conservative

2

Agree

Male

Non-White

16

16

12

2

Liberal

4

Strongly Disagree

Male

White

16

16

5

3

Slight Liberal

18.2 EXPLORATORY DATA ANALYSIS

18.2.1 Entire Sample

df_gss %>% 
  dplyr::select(spanking) %>% 
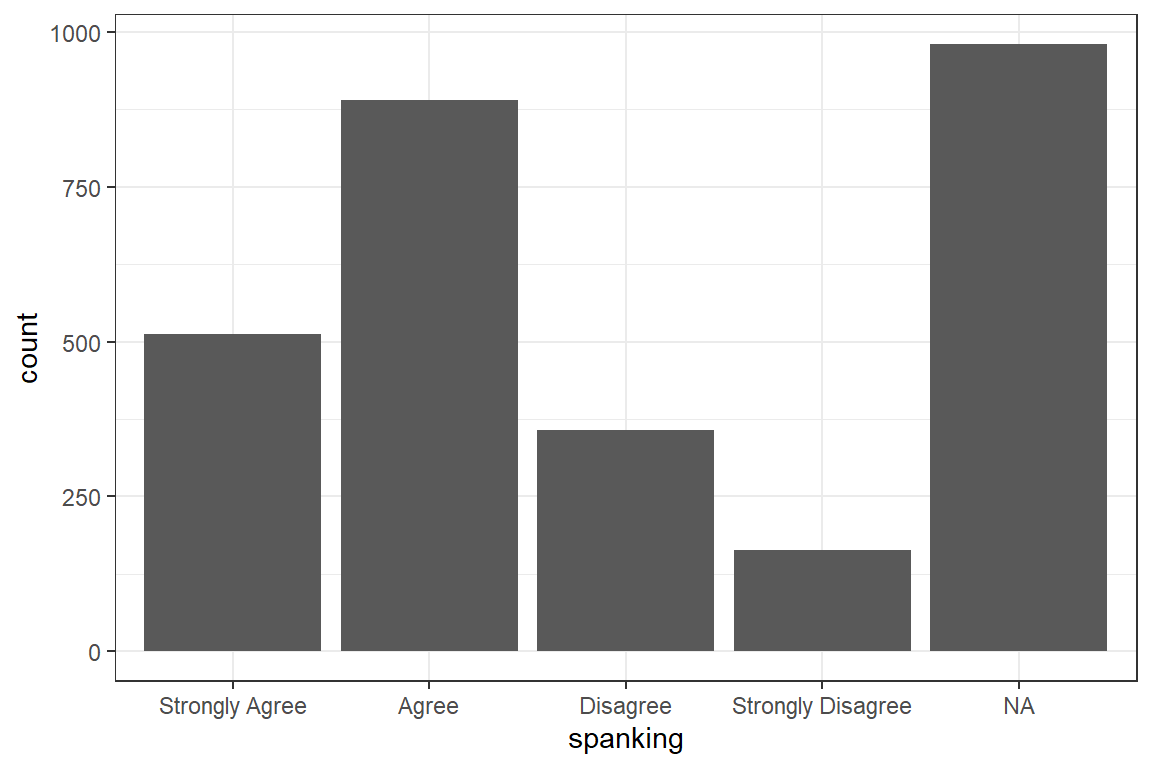
  apaSupp::tab1(caption = "Hoffmann's Example 4.1 Summary of the Spanking Variable",
                general_note = "Full sample included.")
Table 18.2
Hoffmann's Example 4.1 Summary of the Spanking Variable

N = 2,903

spanking

Strongly Agree

512 (26.6%)

Agree

890 (46.3%)

Disagree

357 (18.6%)

Strongly Disagree

164 (8.5%)

Unknown

980

Note. . . Full sample included.

df_gss %>% 
  ggplot(aes(spanking)) +
  geom_bar() +
  theme_bw()

18.2.2 By Education

df_gss %>% 
  dplyr::mutate(spanking = forcats::fct_explicit_na(spanking)) %>% 
  dplyr::select(spanking,
                "Years" = educate,
                "Factor" = educateF) %>% 
  apaSupp::tab1(split = "spanking",
                total = FALSE,
                caption = "Education by Spanking")
Table 18.3
Education by Spanking

Strongly Agree
n = 512 (17.6%)

Agree
n = 890 (30.7%)

Disagree
n = 357 (12.3%)

Strongly Disagree
n = 164 (5.65%)

(Missing)
n = 980 (33.8%)

p-value

Years

12.64 (2.96)

13.40 (2.84)

14.00 (2.74)

14.24 (3.00)

13.32 (2.95)

< .001***

Unknown

1

3

1

0

4

Factor

< .001***

0

0 (0.0%)

2 (0.2%)

0 (0.0%)

0 (0.0%)

2 (0.2%)

3

5 (1.0%)

0 (0.0%)

0 (0.0%)

0 (0.0%)

3 (0.3%)

4

1 (0.2%)

0 (0.0%)

0 (0.0%)

1 (0.6%)

4 (0.4%)

5

4 (0.8%)

5 (0.6%)

0 (0.0%)

1 (0.6%)

3 (0.3%)

6

5 (1.0%)

5 (0.6%)

1 (0.3%)

0 (0.0%)

3 (0.3%)

7

7 (1.4%)

8 (0.9%)

0 (0.0%)

1 (0.6%)

7 (0.7%)

8

25 (4.9%)

15 (1.7%)

5 (1.4%)

2 (1.2%)

33 (3.4%)

9

15 (2.9%)

20 (2.3%)

7 (2.0%)

4 (2.4%)

23 (2.4%)

10

27 (5.3%)

44 (5.0%)

11 (3.1%)

4 (2.4%)

35 (3.6%)

11

39 (7.6%)

42 (4.7%)

16 (4.5%)

5 (3.0%)

53 (5.4%)

12

152 (29.7%)

270 (30.4%)

97 (27.2%)

33 (20.1%)

297 (30.4%)

13

56 (11.0%)

90 (10.1%)

41 (11.5%)

19 (11.6%)

90 (9.2%)

14

56 (11.0%)

111 (12.5%)

41 (11.5%)

19 (11.6%)

112 (11.5%)

15

19 (3.7%)

47 (5.3%)

14 (3.9%)

14 (8.5%)

59 (6.0%)

16

59 (11.5%)

105 (11.8%)

68 (19.1%)

31 (18.9%)

129 (13.2%)

17

13 (2.5%)

45 (5.1%)

14 (3.9%)

6 (3.7%)

42 (4.3%)

18

17 (3.3%)

43 (4.8%)

15 (4.2%)

11 (6.7%)

39 (4.0%)

19

3 (0.6%)

15 (1.7%)

8 (2.2%)

2 (1.2%)

13 (1.3%)

20

8 (1.6%)

20 (2.3%)

18 (5.1%)

11 (6.7%)

29 (3.0%)

Unknown

1

3

1

0

4

Note. Continuous variables are summarized with means (SD) and significant group differences assessed via independent one-way analysis of vaiance (ANOVA). Categorical variables are summarized with counts (%) and significant group differences assessed via Chi-squared tests for independence.

* p < .05. ** p < .01. *** p < .001.

18.2.3 Spanking by Sex

df_gss %>% 
  dplyr::select("sex" = female, 
                "Spanking" = spanking) %>% 
  apaSupp::tab1(split = "sex",
                caption = "Summary of the Spanking Variable by Sex",
                general_note = "Full sample included.")
Table 18.4
Summary of the Spanking Variable by Sex

Total
N = 2903

Male
n = 1285 (44.3%)

Female
n = 1618 (55.7%)

p-value

Spanking

.029*

Strongly Agree

512 (26.6%)

243 (28.8%)

269 (24.9%)

Agree

890 (46.3%)

388 (46.0%)

502 (46.5%)

Disagree

357 (18.6%)

156 (18.5%)

201 (18.6%)

Strongly Disagree

164 (8.5%)

56 (6.6%)

108 (10.0%)

Unknown

980

442

538

Note. . . Full sample included.

* p < .05. ** p < .01. *** p < .001. 

df_gss_model %>% 
  dplyr::select("sex" = female, 
                "Spanking" = spanking) %>% 
  apaSupp::tab1(split = "sex",
                caption = "Summary of the Spanking Variable by Sex",
                general_note = "Compleate casses only.")
Table 18.5
Summary of the Spanking Variable by Sex

Total
N = 1918

Male
n = 841 (43.8%)

Female
n = 1077 (56.2%)

p-value

Spanking

.027*

Strongly Agree

511 (26.6%)

243 (28.9%)

268 (24.9%)

Agree

887 (46.2%)

387 (46.0%)

500 (46.4%)

Disagree

356 (18.6%)

155 (18.4%)

201 (18.7%)

Strongly Disagree

164 (8.6%)

56 (6.7%)

108 (10.0%)

Note. . . Compleate casses only.

* p < .05. ** p < .01. *** p < .001.

18.3 LINEAR REGRESSION - a bad idea here

Linear regression is often ill-suited to fitting a likert rating, such as agreement.

18.3.1 Visualization

df_gss_model %>% 
  ggplot(aes(x = educate,
             y = spankingN)) +                    
  geom_count() +                               # point size relative to over-plotting
  geom_smooth(method = "lm") +                 # add linear regression line (OLS)
  theme_bw() +
  labs(x = "Years of Formal Education",
       y = "Spanking")

Figure 18.1
Hoffmann’s Figure 4.1

Hoffmann's Figure 4.1

18.3.2 Fit the Model

fit_lm <- lm(spankingN ~ educate,
             data = df_gss_model)

summary(fit_lm)

Call:
lm(formula = spankingN ~ educate, data = df_gss_model)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.44768 -0.79947 -0.06955  0.66036  2.41660 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 1.367326   0.093670  14.597  < 2e-16 ***
educate     0.054018   0.006839   7.898 4.73e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.8729 on 1916 degrees of freedom
Multiple R-squared:  0.03153,   Adjusted R-squared:  0.03103 
F-statistic: 62.38 on 1 and 1916 DF,  p-value: 4.73e-15
anova(fit_lm)
# A tibble: 2 × 5
     Df `Sum Sq` `Mean Sq` `F value`  `Pr(>F)`
  <int>    <dbl>     <dbl>     <dbl>     <dbl>
1     1     47.5    47.5        62.4  4.73e-15
2  1916   1460.      0.762      NA   NA

18.3.3 Tabulate Parameters

apaSupp::tab_lm(fit_lm,
                caption = "Hoffmann's Example 4.2")
Table 18.6
Hoffmann's Example 4.2

b

(SE)

p

b∗b^*

η2\eta^2

ηp2\eta^2_p

(Intercept)

1.37

(0.09)

< .001***

educate

0.05

(0.01)

< .001***

0.18

.032

.032

R²

.032

Adjusted R²

.031

Note. N = 1918. b∗b^* = standardize coefficient; η2\eta^2 = semi-partial correlation; ηp2\eta^2_p = partial correlation; p = significance from Wald t-test for parameter estimate.

* p < .05. ** p < .01. *** p < .001.

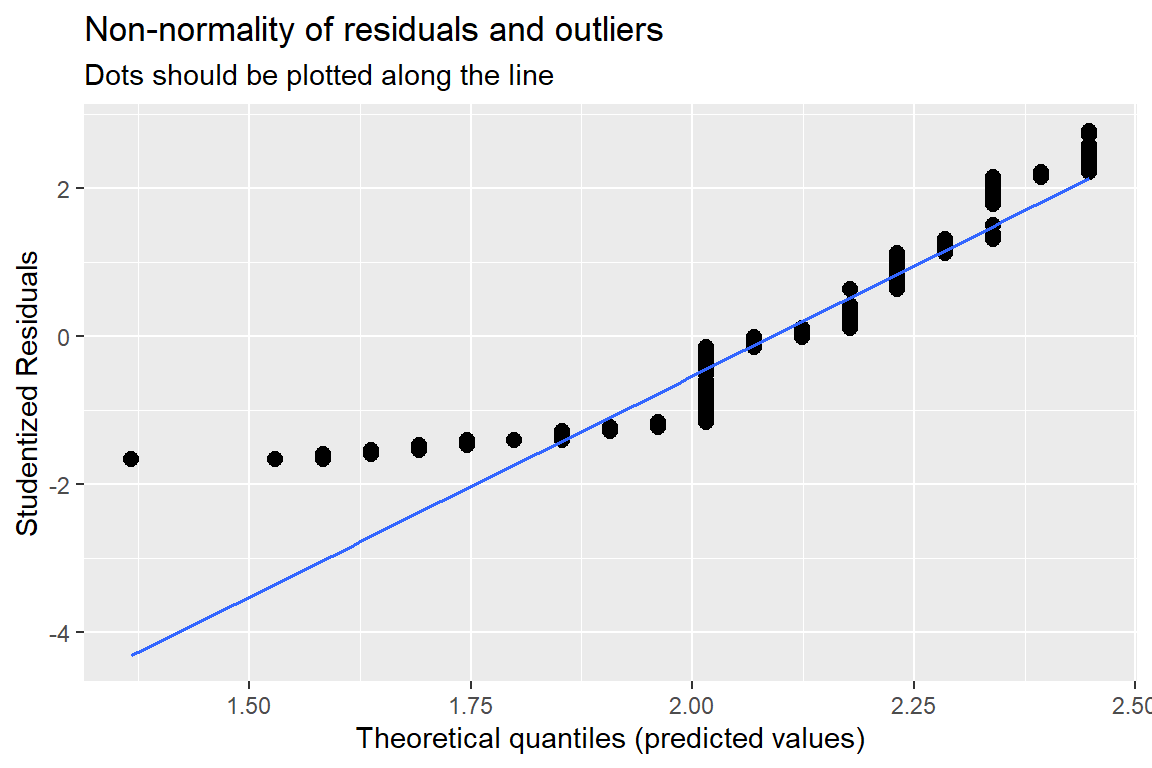
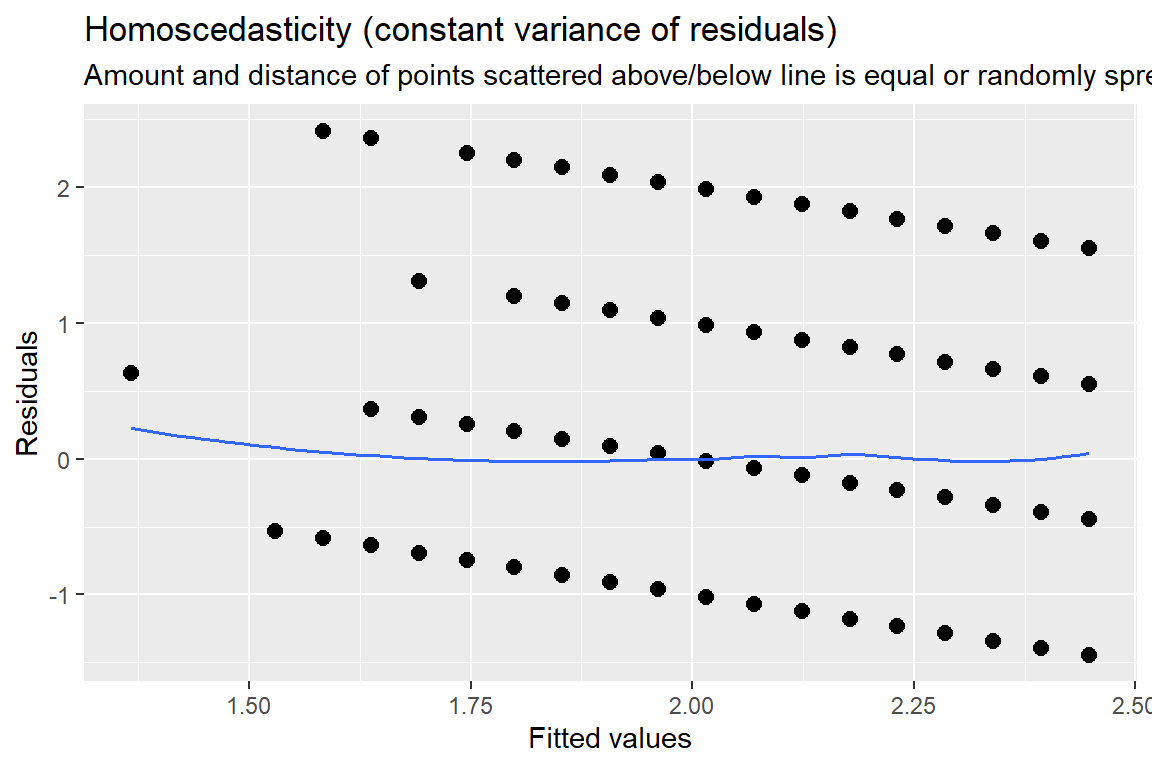
18.3.4 Residual Diagnostics

sjPlot::plot_model(fit_lm, type = "diag")
[[1]]

Figure 18.2
Hoffman’s Figures 4.2 and 4.3 Residual Diagnostics for a linear model on likery dependent variable - YUCK!

Hoffman's Figures 4.2 and 4.3 Residual Diagnostics for a linear model on likery dependent variable - YUCK! 

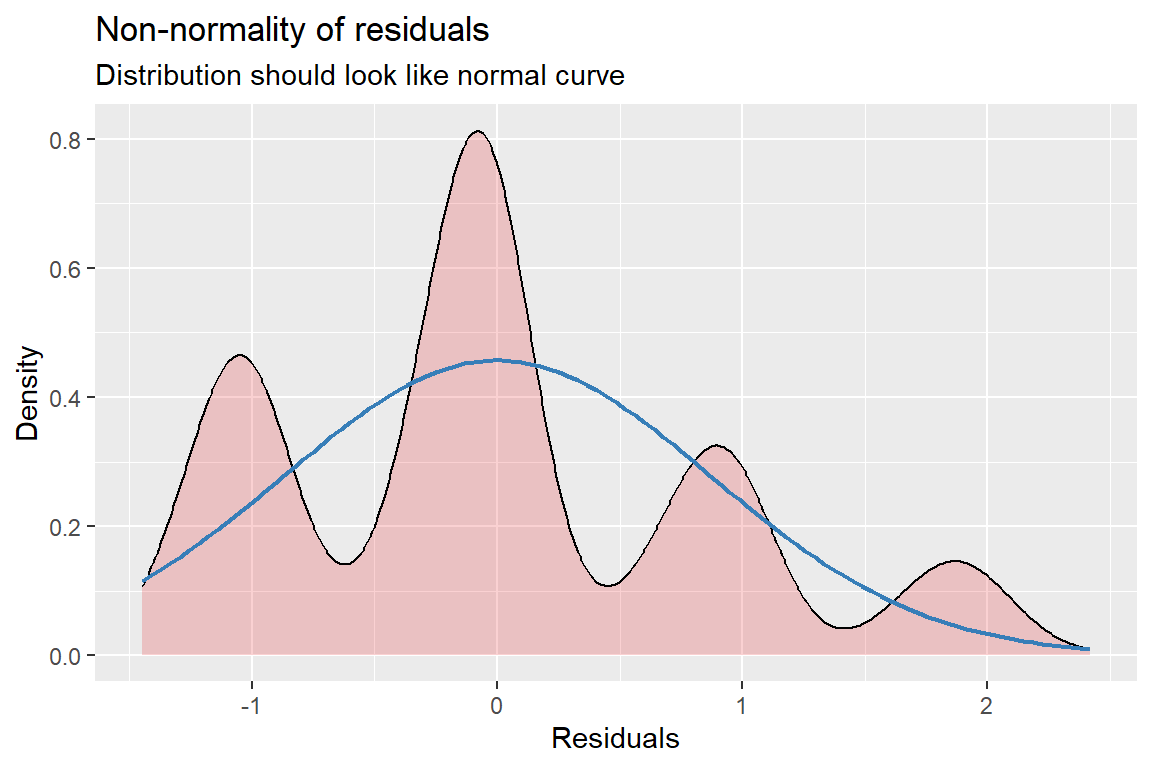
[[2]]

Figure 18.3
Hoffman’s Figures 4.2 and 4.3 Residual Diagnostics for a linear model on likery dependent variable - YUCK!

Hoffman's Figures 4.2 and 4.3 Residual Diagnostics for a linear model on likery dependent variable - YUCK! 

[[3]]

Figure 18.4
Hoffman’s Figures 4.2 and 4.3 Residual Diagnostics for a linear model on likery dependent variable - YUCK!

Hoffman's Figures 4.2 and 4.3 Residual Diagnostics for a linear model on likery dependent variable - YUCK!

18.4 ORDERED LOGISTIC REGRESSION

df_gss_model %>% 
  dplyr::select("sex" = female, 
                "Spanking" = spanking) %>% 
  apaSupp::tab1(split = "sex",
                caption = "Hoffmann's Example 4.3 Crosstabulate DV with Sex",
                general_note = "Compleate casses only.")
Table 18.7
Hoffmann's Example 4.3 Crosstabulate DV with Sex

Total
N = 1918

Male
n = 841 (43.8%)

Female
n = 1077 (56.2%)

p-value

Spanking

.027*

Strongly Agree

511 (26.6%)

243 (28.9%)

268 (24.9%)

Agree

887 (46.2%)

387 (46.0%)

500 (46.4%)

Disagree

356 (18.6%)

155 (18.4%)

201 (18.7%)

Strongly Disagree

164 (8.6%)

56 (6.7%)

108 (10.0%)

Note. . . Compleate casses only.

* p < .05. ** p < .01. *** p < .001.

18.5 Proportional-odds (ordinal) Logistic Regression

This type of logisit regression model forces the predictors to have similar relationship with the outcome (slopes), but different means (intercepts). This is called the proportional odds assumption.

18.5.1 Fit Model 1: Sex

Use polr() function in the base \(R\) MASS package. While outcome variable (dependent variable, “Y”) may be a regular factor, it is preferable to specify it as an ordered factor.

fit_polr_1 <- MASS::polr(spanking ~ female,
                         data = df_gss_model)

summary(fit_polr_1)
Call:
MASS::polr(formula = spanking ~ female, data = df_gss_model)

Coefficients:
              Value Std. Error t value
femaleFemale 0.2116    0.08532    2.48

Intercepts:
                           Value    Std. Error t value 
Strongly Agree|Agree        -0.8967   0.0694   -12.9114
Agree|Disagree               1.1094   0.0711    15.6078
Disagree|Strongly Disagree   2.4922   0.0958    26.0026

Residual Deviance: 4719.394 
AIC: 4727.394

18.5.2 Extract Parameters

18.5.2.1 Logit Scale

fit_polr_1$zeta
      Strongly Agree|Agree             Agree|Disagree 
                -0.8966862                  1.1093754 
Disagree|Strongly Disagree 
                 2.4921855 
fit_polr_1 %>% coef()
femaleFemale 
   0.2116244 
fit_polr_1 %>% confint()
     2.5 %     97.5 % 
0.04451894 0.37901780

18.5.2.2 Odds-Ratio Scale

fit_polr_1$zeta %>% exp()
      Strongly Agree|Agree             Agree|Disagree 
                 0.4079192                  3.0324638 
Disagree|Strongly Disagree 
                12.0876653 
fit_polr_1 %>% coef() %>% exp()
femaleFemale 
    1.235684 
fit_polr_1 %>% confint() %>% exp()
   2.5 %   97.5 % 
1.045525 1.460849

18.5.2.3 Predicted Probabilities

effects::allEffects(fit_polr_1)
 model: spanking ~ female

female effect (probability) for Strongly Agree
female
    Male   Female 
0.289732 0.248186 

female effect (probability) for Agree
female
     Male    Female 
0.4622807 0.4623011 

female effect (probability) for Disagree
female
     Male    Female 
0.1715795 0.1967672 

female effect (probability) for Strongly Disagree
female
      Male     Female 
0.07640782 0.09274572

18.5.3 Tabulate parameters

texreg::knitreg(fit_polr_1,
                custom.model.name = c("b (SE)"),
                custom.coef.map = list("femaleFemale"             = "Female vs. Male",
                                       "Strongly Agree|Agree"     = "strongly agree|agree",
                                       "Agree|Disagree"           = "agree|disagree",
                                       "Disagree|Strongly Disagree" = "disagree|strongly disagree"),
                groups = list("Predictors" = 1,
                              "Cut Values (i.e. threasholds)" = 2:4),
                caption = "Hoffmann's Example 4.4 Ordered Logistic Regression",
                caption.above = TRUE,
                single.row = TRUE,
                digits = 4)
Hoffmann’s Example 4.4 Ordered Logistic Regression
  b (SE)
Predictors  
     Female vs. Male 0.2116 (0.0853)*
Cut Values (i.e. threasholds)  
     strongly agree|agree -0.8967 (0.0694)***
     agree|disagree 1.1094 (0.0711)***
     disagree|strongly disagree 2.4922 (0.0958)***
AIC 4727.3944
BIC 4749.6306
Log Likelihood -2359.6972
Deviance 4719.3944
Num. obs. 1918
***p < 0.001; **p < 0.01; *p < 0.05

18.5.4 Predicted Probabilities

ggeffects::ggeffect(model = fit_polr_1,
                    terms = c("female"))
# A tibble: 8 × 7
  x      predicted std.error conf.low conf.high response.level    group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <chr>             <fct>
1 Male      0.290     0.0694   0.263     0.319  Strongly.Agree    1    
2 Female    0.248     0.0647   0.225     0.273  Strongly.Agree    1    
3 Male      0.462     0.0460   0.440     0.485  Agree             1    
4 Female    0.462     0.0459   0.440     0.485  Agree             1    
5 Male      0.172     0.0708   0.153     0.192  Disagree          1    
6 Female    0.197     0.0653   0.177     0.218  Disagree          1    
7 Male      0.0764    0.0958   0.0642    0.0908 Strongly.Disagree 1    
8 Female    0.0927    0.0889   0.0791    0.109  Strongly.Disagree 1    
ggeffects::ggeffect(model = fit_polr_1,
                    terms = c("female")) %>% 
  dplyr::filter(x == "Female")
# A tibble: 4 × 7
  x      predicted std.error conf.low conf.high response.level    group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <chr>             <fct>
1 Female    0.248     0.0647   0.225      0.273 Strongly.Agree    1    
2 Female    0.462     0.0459   0.440      0.485 Agree             1    
3 Female    0.197     0.0653   0.177      0.218 Disagree          1    
4 Female    0.0927    0.0889   0.0791     0.109 Strongly.Disagree 1

18.5.5 Plot Predicted Probabilities

ggeffects::ggeffect(model = fit_polr_1,
                    terms = c("female")) %>%    # x-axis
  data.frame() %>% 
  ggplot(aes(x = x,
             y = predicted,
             group = response.level,
             color = response.level)) +
  geom_errorbar(aes(ymin = conf.low,
                    ymax = conf.high),
                width = .25) +
  geom_point(size = 4) +
  geom_line(aes(linetype = response.level))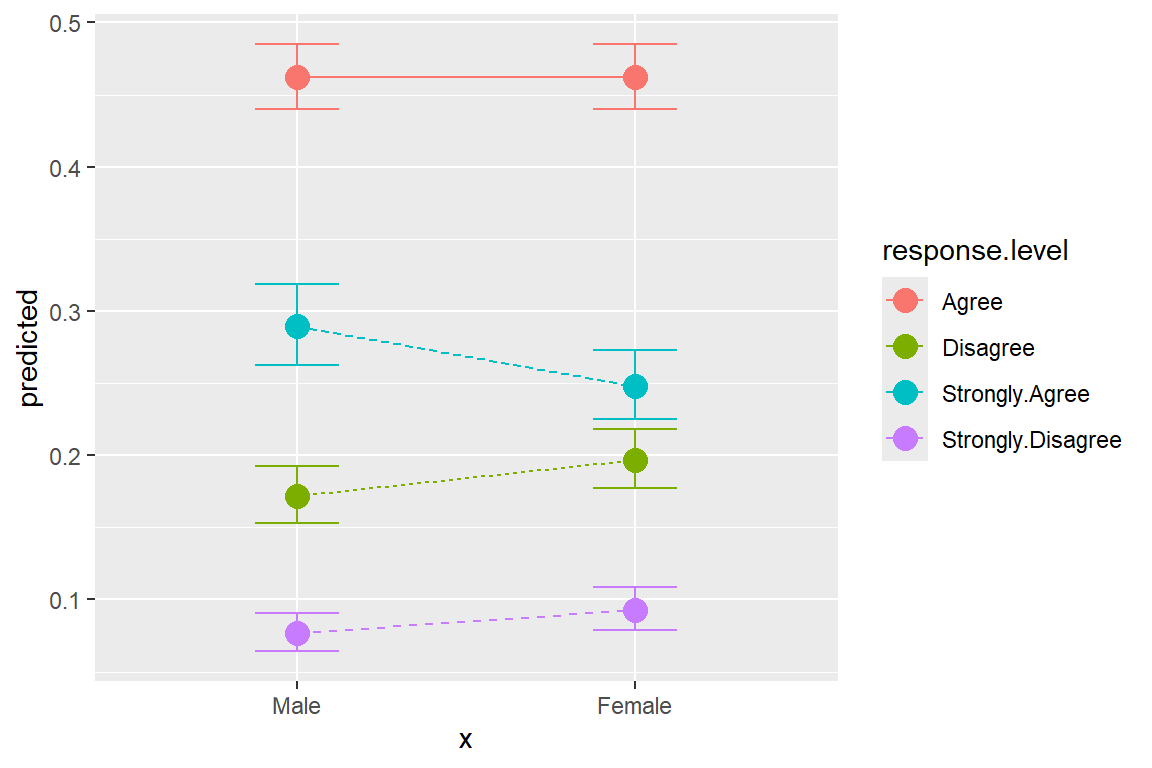 

ggeffects::ggeffect(model = fit_polr_1,
                    terms = c("female")) %>%    # x-axis
  data.frame() %>% 
  dplyr::mutate(response.level = response.level %>% 
                  forcats::fct_reorder(predicted) %>% 
                  forcats::fct_rev()) %>% 
  ggplot(aes(x = x,
             y = predicted,
             group = response.level,
             color = response.level)) +
  geom_errorbar(aes(ymin = conf.low,
                    ymax = conf.high),
                width = .25) +
  geom_point(size = 4) +
  geom_line(aes(linetype = response.level)) +
  theme_bw() +
  labs(x = NULL,
       y = "Predicted Probability",
       color    = "Spanking:",
       shape    = "Spanking:",
       linetype = "Spanking:") +
  theme(legend.key.width = unit(2, "cm")) +
  scale_linetype_manual(values = c("solid", "longdash", "dotdash", "dotted")) +
  scale_shape_manual(values = c(0, 1, 2, 8))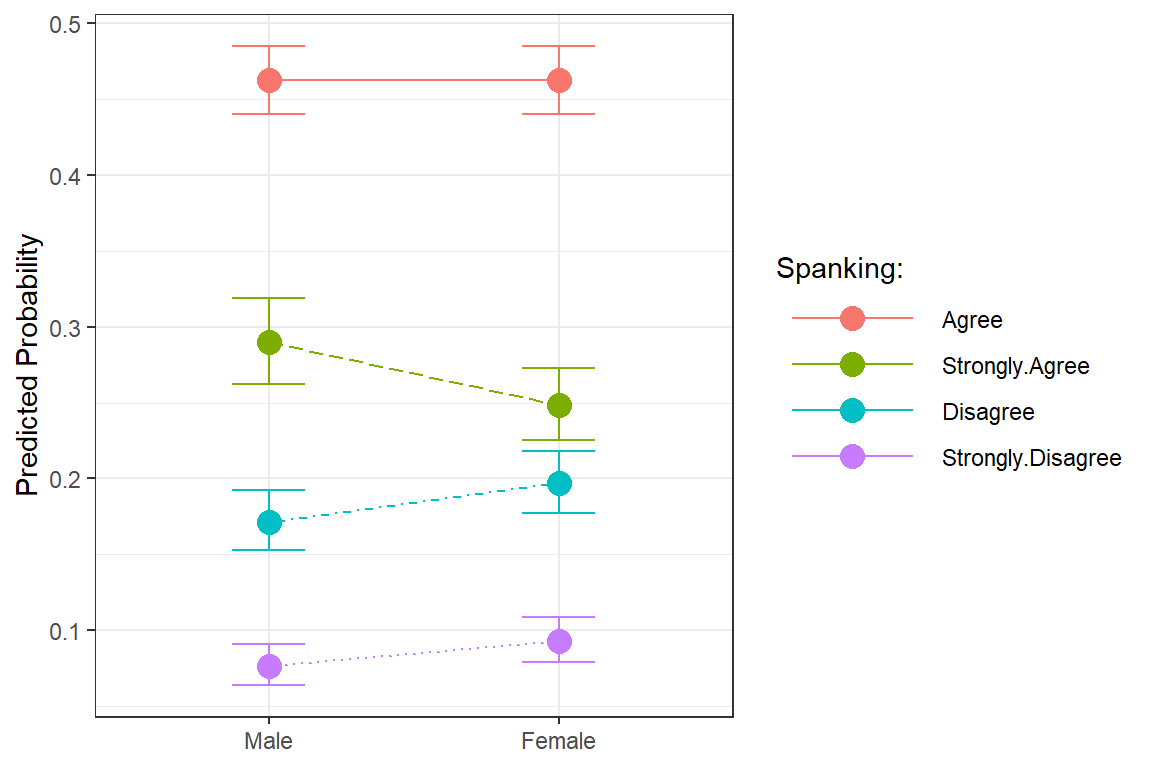

18.5.6 Model Fit and Variance Explained

fit_polr_0 <- MASS::polr(spanking ~ 1,
                         data = df_gss_model)
anova(fit_polr_1, fit_polr_0)
# A tibble: 2 × 7
  Model  `Resid. df` `Resid. Dev` Test     `   Df` `LR stat.` `Pr(Chi)`
  <chr>        <dbl>        <dbl> <chr>      <dbl>      <dbl>     <dbl>
1 1             1915        4726. ""            NA      NA      NA     
2 female        1914        4719. "1 vs 2"       1       6.16    0.0130
performance::performance(fit_polr_1)
Can't calculate log-loss.
# A tibble: 1 × 6
    AIC  AICc   BIC R2_Nagelkerke  RMSE Sigma
  <dbl> <dbl> <dbl>         <dbl> <dbl> <dbl>
1 4727. 4727. 4750.       0.00351  2.05  1.57
performance::r2(fit_polr_1)
  Nagelkerke's R2: 0.004

18.5.7 Assumptions

18.5.7.1 Proportional Odds: Brant Test

The poTest function implements tests proposed by Brant (1990) for proportional odds for logistic models fit by the polr() function in the MASS package.

# Hoffmann's Examle 4.5 (continued...)
car::poTest(fit_polr_1)

Tests for Proportional Odds
MASS::polr(formula = spanking ~ female, data = df_gss_model)

             b[polr] b[>Strongly Agree] b[>Agree] b[>Disagree] Chisquare df
Overall                                                             3.01  2
femaleFemale   0.212              0.204     0.183        0.446      3.01  2
             Pr(>Chisq)
Overall            0.22
femaleFemale       0.22

A significant test statistics provides evidence that the parallel regression assumption has been violated!

18.5.8 Fit Model 2: Sex + Covars

fit_polr_2 <- MASS::polr(spanking ~ female + educate + polviewsN,
                         data = df_gss_model)

summary(fit_polr_2)
Call:
MASS::polr(formula = spanking ~ female + educate + polviewsN, 
    data = df_gss_model)

Coefficients:
               Value Std. Error t value
femaleFemale  0.2532    0.08825   2.869
educate       0.1153    0.01564   7.374
polviewsN    -0.2215    0.03248  -6.818

Intercepts:
                           Value   Std. Error t value
Strongly Agree|Agree       -0.2977  0.2671    -1.1146
Agree|Disagree              1.7845  0.2706     6.5935
Disagree|Strongly Disagree  3.1926  0.2793    11.4312

Residual Deviance: 4396.504 
AIC: 4408.504 
(97 observations deleted due to missingness)

18.5.9 Extract Parameters

18.5.9.1 Logit Scale

fit_polr_2$zeta
      Strongly Agree|Agree             Agree|Disagree 
                -0.2976843                  1.7844863 
Disagree|Strongly Disagree 
                 3.1926342 
fit_polr_2 %>% coef()
femaleFemale      educate    polviewsN 
   0.2532132    0.1152980   -0.2214577 
fit_polr_2 %>% confint()
                   2.5 %     97.5 %
femaleFemale  0.08039420  0.4263963
educate       0.08472724  0.1460403
polviewsN    -0.28526298 -0.1579046

18.5.9.2 Odds-Ratio Scale

fit_polr_2$zeta %>% exp()
      Strongly Agree|Agree             Agree|Disagree 
                 0.7425358                  5.9565193 
Disagree|Strongly Disagree 
                24.3524926 
fit_polr_2 %>% coef() %>% exp()
femaleFemale      educate    polviewsN 
   1.2881578    1.1222079    0.8013498 
fit_polr_2 %>% confint() %>% exp()
                 2.5 %    97.5 %
femaleFemale 1.0837142 1.5317277
educate      1.0884202 1.1572429
polviewsN    0.7518165 0.8539312

18.5.10 Tabulate parameters

texreg::knitreg(fit_polr_2,
                custom.model.name = c("b (SE)"),
                custom.coef.map = list("femaleFemale"             = "Female vs. Male",
                                       "educate"                  = "Years of Education",
                                       "polviewsN"                = "Level of Polytical Views",
                                       "Strongly Agree|Agree"     = "Strongly Agree|Agree",
                                       "Agree|Disagree"           = "Agree|Disagree",
                                       "Disagree|Strongly Disagree" = "Disagree|Strongly Disagree"),
                groups = list("Predictors" = 1:3,
                              "Cut Values" = 4:6),
                caption = "Hoffmann's Example 4.7 Ordered Logistic Regression",
                caption.above = TRUE,
                single.row = TRUE,
                digits = 4)
Hoffmann’s Example 4.7 Ordered Logistic Regression
  b (SE)
Predictors  
     Female vs. Male 0.2532 (0.0883)**
     Years of Education 0.1153 (0.0156)***
     Level of Polytical Views -0.2215 (0.0325)***
Cut Values  
     Strongly Agree|Agree -0.2977 (0.2671)
     Agree|Disagree 1.7845 (0.2706)***
     Disagree|Strongly Disagree 3.1926 (0.2793)***
AIC 4408.5038
BIC 4441.5466
Log Likelihood -2198.2519
Deviance 4396.5038
Num. obs. 1821
***p < 0.001; **p < 0.01; *p < 0.05

18.5.11 Predicted Probabilities

The ggeffects package computes estimated marginal means (predicted values) for the response, at the margin of specific values or levels from certain model terms, i.e. it generates predictions by a model by holding the non-focal variables constant and varying the focal variable(s).

  • ggpredict() uses predict() for generating predictions
    • factors: uses the reference level
  • ggeffect() computes marginal effects by internally calling effects::Effect()
    • factors: compute a kind of “average” value, which represents the proportions of each factor’s category
  • ggemmeans() uses emmeans::emmeans()
    • factors: compute a kind of “average” value, which represents the proportions of each factor’s category

Use condition to set a specific level for factors in ggemmeans(), so factors are not averaged over their categories, but held constant at a given level.

ggeffects::ggpredict() Adjusted for: * educate = 13.51 The grand mean value * polviewsN = 4.17 The grand mean value

## Hoffmann's Example 4.8 (continues...approximated)
ggeffects::ggpredict(model = fit_polr_2,
                    terms = c("female")) 
# A tibble: 8 × 7
  x      predicted std.error conf.low conf.high response.level    group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <chr>             <fct>
1 Male      0.283      0.253   0.193      0.393 Strongly Agree    1    
2 Male      0.477      0.253   0.357      0.600 Agree             1    
3 Male      0.169      0.253   0.110      0.250 Disagree          1    
4 Male      0.0718     0.253   0.0450     0.113 Strongly Disagree 1    
5 Female    0.234      0.276   0.151      0.344 Strongly Agree    1    
6 Female    0.476      0.276   0.346      0.610 Agree             1    
7 Female    0.199      0.276   0.126      0.299 Disagree          1    
8 Female    0.0906     0.276   0.0548     0.146 Strongly Disagree 1    
ggeffects::ggpredict(model = fit_polr_2,
                    terms = c("female")) %>% 
  data.frame()
# A tibble: 8 × 7
  x      predicted std.error conf.low conf.high response.level    group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <chr>             <fct>
1 Male      0.283      0.253   0.193      0.393 Strongly Agree    1    
2 Male      0.477      0.253   0.357      0.600 Agree             1    
3 Male      0.169      0.253   0.110      0.250 Disagree          1    
4 Male      0.0718     0.253   0.0450     0.113 Strongly Disagree 1    
5 Female    0.234      0.276   0.151      0.344 Strongly Agree    1    
6 Female    0.476      0.276   0.346      0.610 Agree             1    
7 Female    0.199      0.276   0.126      0.299 Disagree          1    
8 Female    0.0906     0.276   0.0548     0.146 Strongly Disagree 1

18.6 Hoffmann’s Example 4.8 (continues…approximated)

ggeffects::ggpredict() Adjusted for: * female = male The reference category * polviewsN = 4.17 The grand mean value

ggeffects::ggpredict(model = fit_polr_2,
                    terms = c("educate [10, 16]",    # 1st = x
                              "female")) %>%         # 2nd = group
  data.frame() %>% 
  dplyr::filter(group == "Male")
# A tibble: 8 × 7
      x predicted std.error conf.low conf.high response.level    group
  <dbl>     <dbl>     <dbl>    <dbl>     <dbl> <chr>             <fct>
1    10    0.371      0.209   0.282     0.471  Strongly Agree    Male 
2    10    0.454      0.209   0.356     0.556  Agree             Male 
3    10    0.125      0.209   0.0868    0.177  Disagree          Male 
4    10    0.0491     0.209   0.0331    0.0722 Strongly Disagree Male 
5    16    0.228      0.287   0.144     0.342  Strongly Agree    Male 
6    16    0.475      0.287   0.340     0.614  Agree             Male 
7    16    0.203      0.287   0.127     0.309  Disagree          Male 
8    16    0.0935     0.287   0.0555    0.153  Strongly Disagree Male

ggeffects::ggeffect() Adjusted for: * female computed a kind of “average” value, which represents the proportions of male/female * polviewsN = 4.17 The grand mean value

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("educate [10, 16]")) %>% 
  data.frame()
# A tibble: 8 × 7
      x predicted std.error conf.low conf.high response.level    group
  <dbl>     <dbl>     <dbl>    <dbl>     <dbl> <chr>             <fct>
1    10    0.339     0.0744   0.307     0.372  Strongly.Agree    1    
2    16    0.204     0.0692   0.183     0.227  Strongly.Agree    1    
3    10    0.465     0.0498   0.441     0.490  Agree             1    
4    16    0.469     0.0487   0.445     0.493  Agree             1    
5    10    0.139     0.0793   0.122     0.159  Disagree          1    
6    16    0.221     0.0663   0.199     0.244  Disagree          1    
7    10    0.0561    0.105    0.0461    0.0682 Strongly.Disagree 1    
8    16    0.106     0.0885   0.0908    0.124  Strongly.Disagree 1    
ggeffects::ggemmeans(model = fit_polr_2,
                     terms = c("educate [10, 16]"),
                     condition = c(female = "Female")) %>% 
  data.frame()
# A tibble: 8 × 7
      x predicted std.error conf.low conf.high response.level    group
  <dbl>     <dbl>     <dbl>    <dbl>     <dbl> <fct>             <fct>
1    10    0.314    0.0178    0.279     0.349  Strongly Agree    1    
2    10    0.472    0.0124    0.448     0.496  Agree             1    
3    10    0.151    0.0107    0.130     0.172  Disagree          1    
4    10    0.0624   0.00641   0.0498    0.0749 Strongly Disagree 1    
5    16    0.187    0.0124    0.162     0.211  Strongly Agree    1    
6    16    0.461    0.0125    0.437     0.486  Agree             1    
7    16    0.235    0.0130    0.209     0.260  Disagree          1    
8    16    0.117    0.0100    0.0976    0.137  Strongly Disagree 1

Predictions for specific values: females with 10 or 16 years education

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("female",                 # 1st var = `x`
                              "educate [10, 16]")) %>%  # 2nd var = `group`
  data.frame()
# A tibble: 16 × 7
   x      predicted std.error conf.low conf.high response.level    group
   <fct>      <dbl>     <dbl>    <dbl>     <dbl> <chr>             <dbl>
 1 Male      0.371     0.0909   0.331     0.414  Strongly.Agree       10
 2 Female    0.314     0.0825   0.281     0.350  Strongly.Agree       10
 3 Male      0.228     0.0818   0.201     0.258  Strongly.Agree       16
 4 Female    0.187     0.0820   0.163     0.212  Strongly.Agree       16
 5 Male      0.454     0.0544   0.428     0.481  Agree                10
 6 Female    0.472     0.0496   0.448     0.496  Agree                10
 7 Male      0.475     0.0489   0.451     0.499  Agree                16
 8 Female    0.461     0.0504   0.437     0.486  Agree                16
 9 Male      0.125     0.0937   0.106     0.147  Disagree             10
10 Female    0.151     0.0834   0.132     0.174  Disagree             10
11 Male      0.203     0.0756   0.180     0.228  Disagree             16
12 Female    0.235     0.0721   0.210     0.261  Disagree             16
13 Male      0.0491    0.120    0.0392    0.0613 Strongly.Disagree    10
14 Female    0.0624    0.110    0.0509    0.0762 Strongly.Disagree    10
15 Male      0.0935    0.101    0.0780    0.112  Strongly.Disagree    16
16 Female    0.117     0.0968   0.0990    0.138  Strongly.Disagree    16
ggeffects::ggemmeans(model = fit_polr_2,
                     terms = "female",
                     condition = c(educate = 12,
                                   polviewsN  = 4.5)) 
# A tibble: 8 × 7
  x      predicted std.error conf.low conf.high response.level    group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <fct>             <fct>
1 Male      0.335    0.0169    0.302     0.368  Strongly Agree    1    
2 Male      0.467    0.0124    0.442     0.491  Agree             1    
3 Male      0.141    0.00969   0.122     0.160  Disagree          1    
4 Male      0.0570   0.00571   0.0458    0.0682 Strongly Disagree 1    
5 Female    0.281    0.0141    0.254     0.309  Strongly Agree    1    
6 Female    0.477    0.0121    0.453     0.501  Agree             1    
7 Female    0.169    0.0101    0.149     0.189  Disagree          1    
8 Female    0.0723   0.00653   0.0595    0.0851 Strongly Disagree 1

18.6.1 Plot Predicted Probabilites

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("educate [10, 16]",   # x-axis
                              "female")) %>%        # lines by group
  data.frame() %>%  
  ggplot(aes(x = x,
             y = predicted,
             color = group,
             shape = group)) +
  geom_point(size = 4) +
  geom_line(aes(linetype = group)) +
  facet_wrap(~ response.level)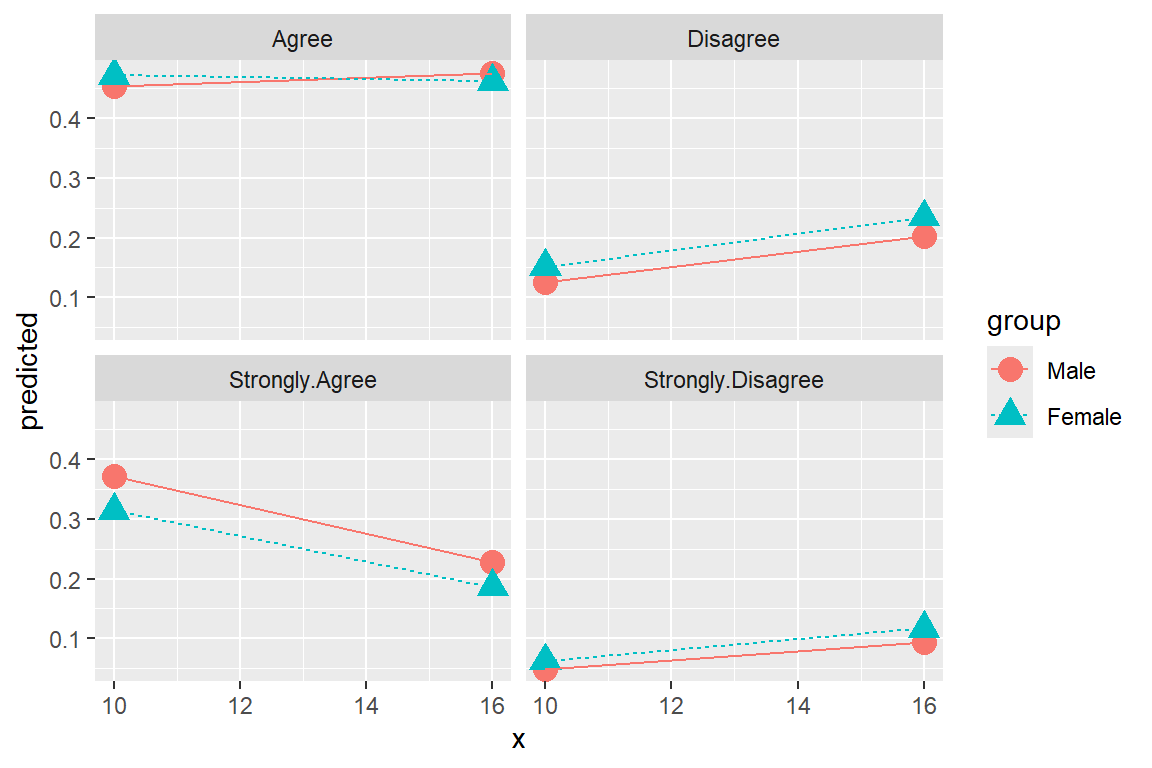

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("educate [10, 16]",   # x-axis
                              "female")) %>%        # lines by group
  data.frame() %>% 
  dplyr::filter(response.level == "Strongly.Agree") %>% 
  ggplot(aes(x = x,
             y = predicted,
             color = group)) +
  geom_point(size = 4) +
  geom_line(aes(linetype = group))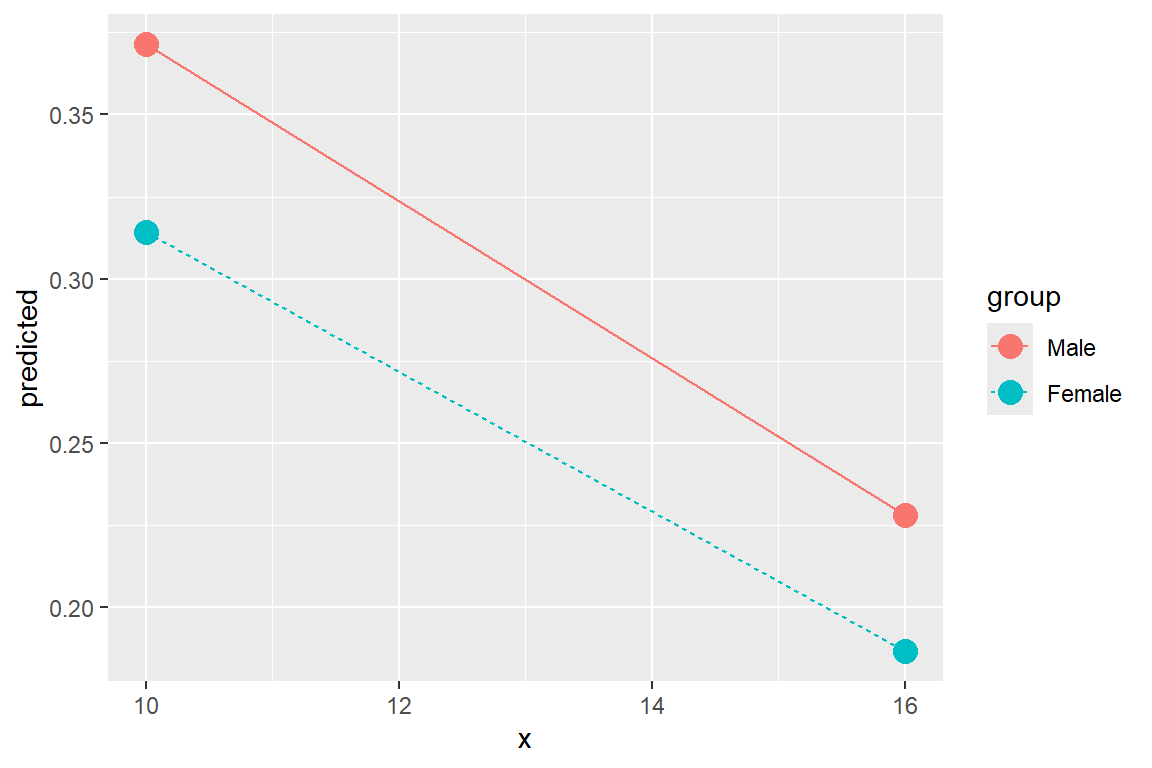 

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("educate [10, 16]",   # x-axis
                              "female")) %>%        # lines by group
  data.frame() %>% 
  dplyr::filter(response.level == "Strongly.Agree") %>% 
  ggplot(aes(x = x,
             y = predicted,
             color = group,
             shape = group)) +
  geom_errorbar(aes(ymin = conf.low,
                    ymax = conf.high),
                width = .5,
                position = position_dodge(width =.25)) +
  geom_point(size = 4,
             position = position_dodge(width =.25)) +
  geom_line(aes(linetype = group),
            position = position_dodge(width =.25)) +
  theme_bw() +
  labs(x = "Education, years",
       y = "Predicted Probability for Strongly Agree",
       color = NULL,
       shape = NULL,
       linetype = NULL)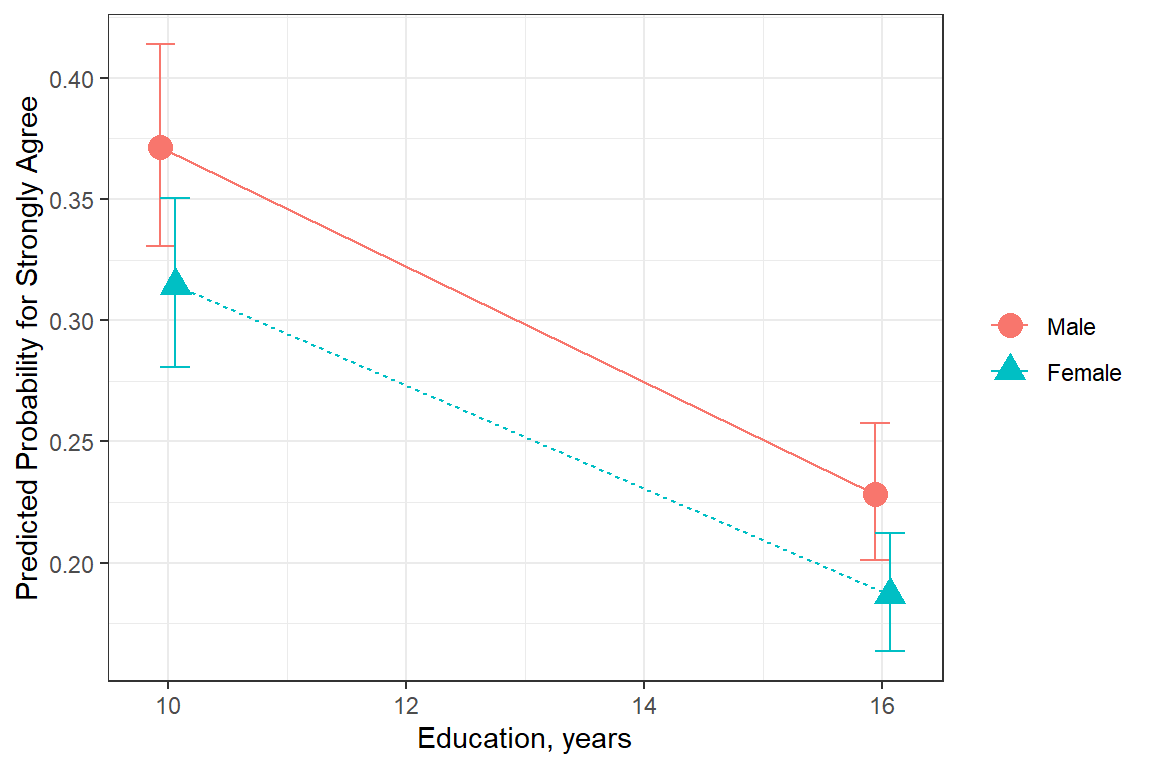

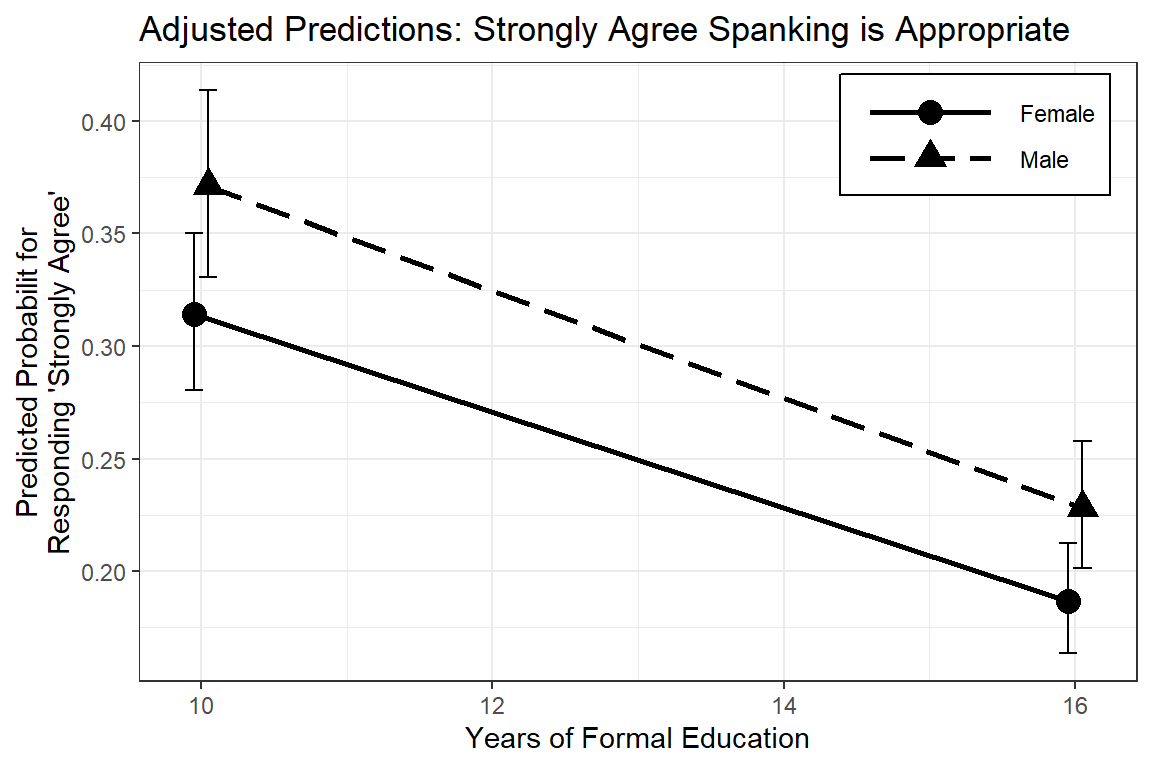
ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("educate [10, 16]",   # x-axis
                              "female")) %>%        # lines by group
  data.frame() %>% 
  dplyr::mutate(group = forcats::fct_rev(group)) %>% 
  dplyr::filter(response.level == "Strongly.Agree") %>% 
  ggplot(aes(x = x,
             y = predicted,
             shape = group)) +
  geom_errorbar(aes(ymin = conf.low,
                    ymax = conf.high),
                width = .25,
                position = position_dodge(.2)) +
  geom_point(size = 4,
                position = position_dodge(.2)) +
  geom_line(aes(linetype = group),
            size = 1,
            position = position_dodge(.2)) +
  theme_bw() + 
  theme(legend.position = c(1, 1),
        legend.justification = c(1.1, 1.1),
        legend.key.width = unit(2, "cm"),
        legend.background = element_rect(color = "black")) +
  scale_linetype_manual(values = c("solid", "longdash")) +
  labs(x = "Years of Formal Education",
       y = "Predicted Probabilit for\nResponding 'Strongly Agree'",
       color = NULL,
       shape = NULL,
       linetype = NULL,
       title = "Adjusted Predictions: Strongly Agree Spanking is Appropriate")

Figure 18.5
Hoffmann’s Figure 4.4

Hoffmann's Figure 4.4 
ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("female")) %>%        # lines by group
  data.frame() %>% 
  dplyr::filter(response.level %in% c("Strongly.Agree",
                                      "Strongly.Disagree")) %>% 
  dplyr::mutate(resonse.level = factor(response.level)) %>% 
  ggplot(aes(x = x,
             y = predicted,
             fill = resonse.level)) +
  geom_col(position = position_dodge())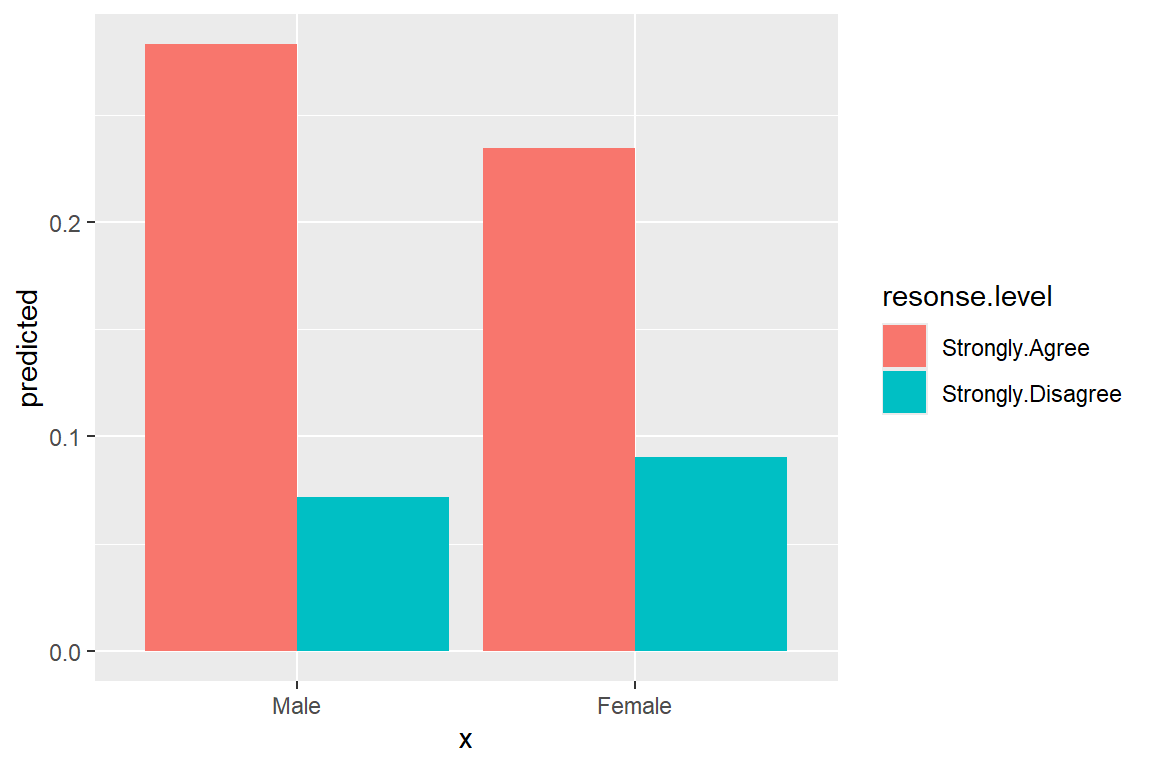 

ggeffects::ggeffect(model = fit_polr_2,
                    terms = c("female")) %>%        # lines by group
  data.frame() %>% 
  dplyr::filter(response.level %in% c("Strongly.Agree",
                                      "Strongly.Disagree")) %>% 
  dplyr::mutate(resonse.level = factor(response.level)) %>% 
  ggplot(aes(x = forcats::fct_rev(x),
             y = predicted,
             fill = resonse.level)) +
  geom_col(position = position_dodge()) +
  theme_bw() +
  theme(legend.position = "bottom") +
  scale_fill_manual(values = c("gray30", "gray70")) +
  labs(x = NULL,
       y = "Predicted Probability of Response",
       fill = NULL,
       title = "Attitues towareds Spanking, by Sex")

Figure 18.6
Hoffmann’s Figure 4.5

Hoffmann's Figure 4.5

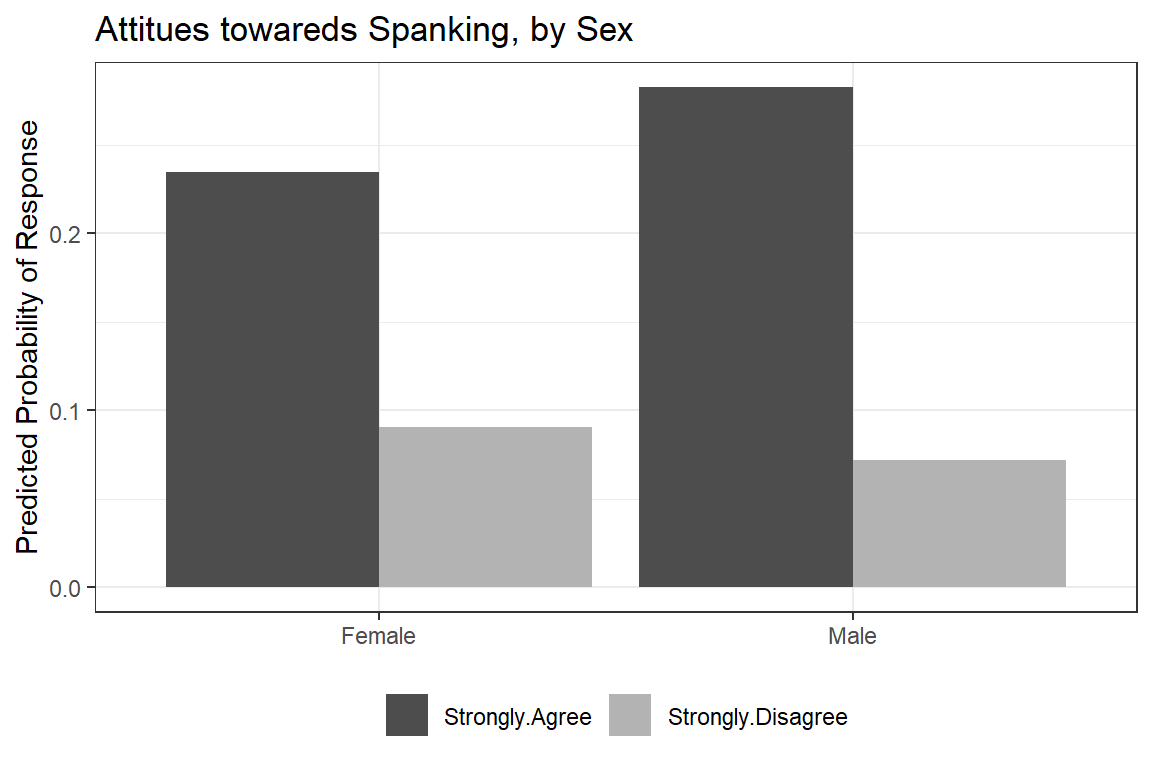
18.6.2 Model Fit and Variance Explained

fit_polr_1redeo <- MASS::polr(spanking ~ female,
                         data = df_gss_model %>% 
                           dplyr::filter(complete.cases(educate, polviewsN)))
anova(fit_polr_2, fit_polr_1redeo)
# A tibble: 2 × 7
  Model              `Resid. df` `Resid. Dev` Test  `   Df` `LR stat.` `Pr(Chi)`
  <chr>                    <dbl>        <dbl> <chr>   <dbl>      <dbl>     <dbl>
1 female                    1817        4501. ""         NA        NA         NA
2 female + educate …        1815        4397. "1 v…       2       105.         0
performance::compare_performance(fit_polr_2, fit_polr_1redeo, rank = TRUE)
# A tibble: 2 × 9
  Name            Model R2_Nagelkerke  RMSE Sigma   AIC_wt  AICc_wt   BIC_wt
  <chr>           <chr>         <dbl> <dbl> <dbl>    <dbl>    <dbl>    <dbl>
1 fit_polr_2      polr        0.0647   2.06  1.56 1   e+ 0 1   e+ 0 1   e+ 0
2 fit_polr_1redeo polr        0.00384  2.06  1.57 1.32e-22 1.34e-22 3.26e-20
# ℹ 1 more variable: Performance_Score <dbl>

18.6.3 Assumptions

18.6.3.1 Proportional Odds: Brant Test

The poTest function implements tests proposed by Brant (1990) for proportional odds for logistic models fit by the polr() function in the MASS package.

# Hoffmann's Example 4.8
car::poTest(fit_polr_2)

Tests for Proportional Odds
MASS::polr(formula = spanking ~ female + educate + polviewsN, 
    data = df_gss_model)

             b[polr] b[>Strongly Agree] b[>Agree] b[>Disagree] Chisquare df
Overall                                                             8.80  6
femaleFemale  0.2532             0.2342    0.2180       0.4719      2.64  2
educate       0.1153             0.1248    0.1036       0.0927      1.17  2
polviewsN    -0.2215            -0.1622   -0.2558      -0.2872      4.85  2
             Pr(>Chisq)  
Overall           0.185  
femaleFemale      0.268  
educate           0.558  
polviewsN         0.089 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

A significant test statistics provides evidence that the parallel regression assumption has been violated!