3 D&H Ch3a - Multiple Regression: “Weight”

Compiled: October 15, 2025

Darlington & Hayes, Chapter 3’s first example

Darlington, Richard B., and Andrew F. Hayes. Regression Analysis and Linear Models : Concepts, Applications, and Implementation, Guilford Publications, 2016. ProQuest Ebook Central, http://ebookcentral.proquest.com/lib/usu/detail.action?docID=4652287. Created from usu on 2025-01-29 01:13:21.

Outside resource * https://www.harshaash.com/R/part-and-partial-corr/ * https://dstanley4.github.io/psyc4780bookdown/multiple-regression.html

Reference: 

# install.packages("remotes")
# remotes::install_github("sarbearschwartz/apaSupp") # 9/17/2025

library(tidyverse)  
library(flextable)
library(apaSupp)       # not on CRAN, get from GitHub (above) 
library(interactions) 
library(effectsize)
library(parameters)
library(car)
library(emmeans)

3.1 PURPOSE

3.1.1 Research Question

How is weight loss associationed with exercise frequency and food intake?

3.1.2 Data Description

Suppose you conducted a study examining the relationship between food consumption and weight loss among people enrolled (n = 10) in a month-long healthy living class.

Dependent Variable (DV)

  • loss average weight loss in hundreds of grams per week

Independent Variables (IVs)

  • exer average weekly hours of exercise

  • diet average daily food consumption (in 100s of calories about the recommended minimum of 1,000 calories required to maintain good health)

  • meta metabolic rate

Manually enter the data set provided on page 44 in Table 3.1 

df_loss <- tibble::tribble(~id, ~exer, ~diet, ~meta, ~loss,
                           1, 0, 2, 15,  6, 
                           2, 0, 4, 14,  2,
                           3, 0, 6, 19,  4,
                           4, 2, 2, 15,  8,
                           5, 2, 4, 21,  9,
                           6, 2, 6, 23,  8,
                           7, 2, 8, 21,  5,
                           8, 4, 4, 22, 11,
                           9, 4, 6, 24, 13,
                           10, 4, 8, 26,  9)
df_loss %>% 
  dplyr::select("ID" = id,
                "Exercise\nFrequency" = exer,
                "Food\nIntake" = diet,
                "Weight\nLoss" = loss) %>% 
  flextable::flextable() %>% 
  apaSupp::theme_apa(caption = "D&H Table 3.1: Exercise, Food Intake, and Weight Loss") %>% 
  flextable::colformat_double(digits = 0) %>% 
  flextable::footnote(part = "header", 
                      i = 1, j = 2:4, 
                      value = flextable::as_paragraph(c("Weekly average of hours/day",
                                                        "Daily average of 100s of calories above recommendation",
                                                        "Weekly average of 100s of grams/week")))
Table 3.1
D&H Table 3.1: Exercise, Food Intake, and Weight Loss

ID

Exercise
Frequency1

Food
Intake2

Weight
Loss3

1

0

2

6

2

0

4

2

3

0

6

4

4

2

2

8

5

2

4

9

6

2

6

8

7

2

8

5

8

4

4

11

9

4

6

13

10

4

8

9

1Weekly average of hours/day

2Daily average of 100s of calories above recommendation

3Weekly average of 100s of grams/week

3.2 EXPLORATORY DATA ANALYSIS

3.2.1 Summary Statistics

3.2.1.1 Univariate

df_loss %>% 
  dplyr::select("Exercise Frequency" = exer,
                "Food Intake" = diet,
                "Metabolic Rate" = meta,
                "Weight Loss" = loss) %>% 
  apaSupp::tab_desc(caption = "Summary Statistics",
                    general_not = "Exercise captures daily average hours.  Food intake is the average of 100's of calories above the recommendation.  Metabolism is the metobalic rate. Weight loss is average weekly weight lost in 100s of grams.")
Table 3.2
Summary Statistics

NA

M

SD

min

Q1

Mdn

Q3

max

Exercise Frequency

0

2.00

1.63

0.00

0.50

2.00

3.50

4.00

Food Intake

0

5.00

2.16

2.00

4.00

5.00

6.00

8.00

Metabolic Rate

0

20.00

4.14

14.00

16.00

21.00

22.75

26.00

Weight Loss

0

7.50

3.31

2.00

5.25

8.00

9.00

13.00

Note. N = 10. NA = not available or missing; Mdn = median; Q1 = 25th percentile; Q3 = 75th percentile. Exercise captures daily average hours. Food intake is the average of 100's of calories above the recommendation. Metabolism is the metobalic rate. Weight loss is average weekly weight lost in 100s of grams.

3.2.1.2 Bivariate

df_loss %>% 
  dplyr::select("Weight Loss" = loss,
                "Exercise Frequency" = exer,
                "Food Intake" = diet) %>% 
  apaSupp::tab_cor(caption = "Correlations",
                   general_note = "Exercise captures daily average hours.  Food intake is the average of 100's of calories above the recommendation.  Weight loss is average weekly weight lost in 100s of grams.") %>% 
  flextable::hline(i = 2)
Table 3.3
Correlations

Variable Pair

r

p

Weight Loss

Exercise Frequency

.860

.001**

Weight Loss

Food Intake

.047

.898

Exercise Frequency

Food Intake

.380

.282

Note. N = 10. r = Pearson's Product-Moment correlation coefficient.Exercise captures daily average hours. Food intake is the average of 100's of calories above the recommendation. Weight loss is average weekly weight lost in 100s of grams.

* p < .05. ** p < .01. *** p < .001.

3.2.2 Visualizations

3.2.2.1 Univariate

df_loss %>% 
  dplyr::select(id, 
                "Weight Loss\n(100 g/day)" = loss,
                "Exercise Frequency\n(hr/day)" = exer,
                "Food Intake\n(100 cal/day above 1000)" = diet,
                "Metabolic Rate" = meta) %>% 
  tidyr::pivot_longer(cols = -id) %>% 
  ggplot(aes(value)) +
  geom_histogram(binwidth = 1,
                 color = "black",
                 alpha = .25) +
  theme_bw() +
  facet_wrap(~ name,
             scale = "free_x") +
  labs(x = NULL,
       y = "Count")

Figure 3.1
Univariate Distibution on Continuous Measures

Univariate Distibution on Continuous Measures

3.2.2.2 Bivariate

df_loss %>% 
  ggplot(aes(x = diet,
             y = loss)) +
  geom_point(aes(shape = factor(exer)))

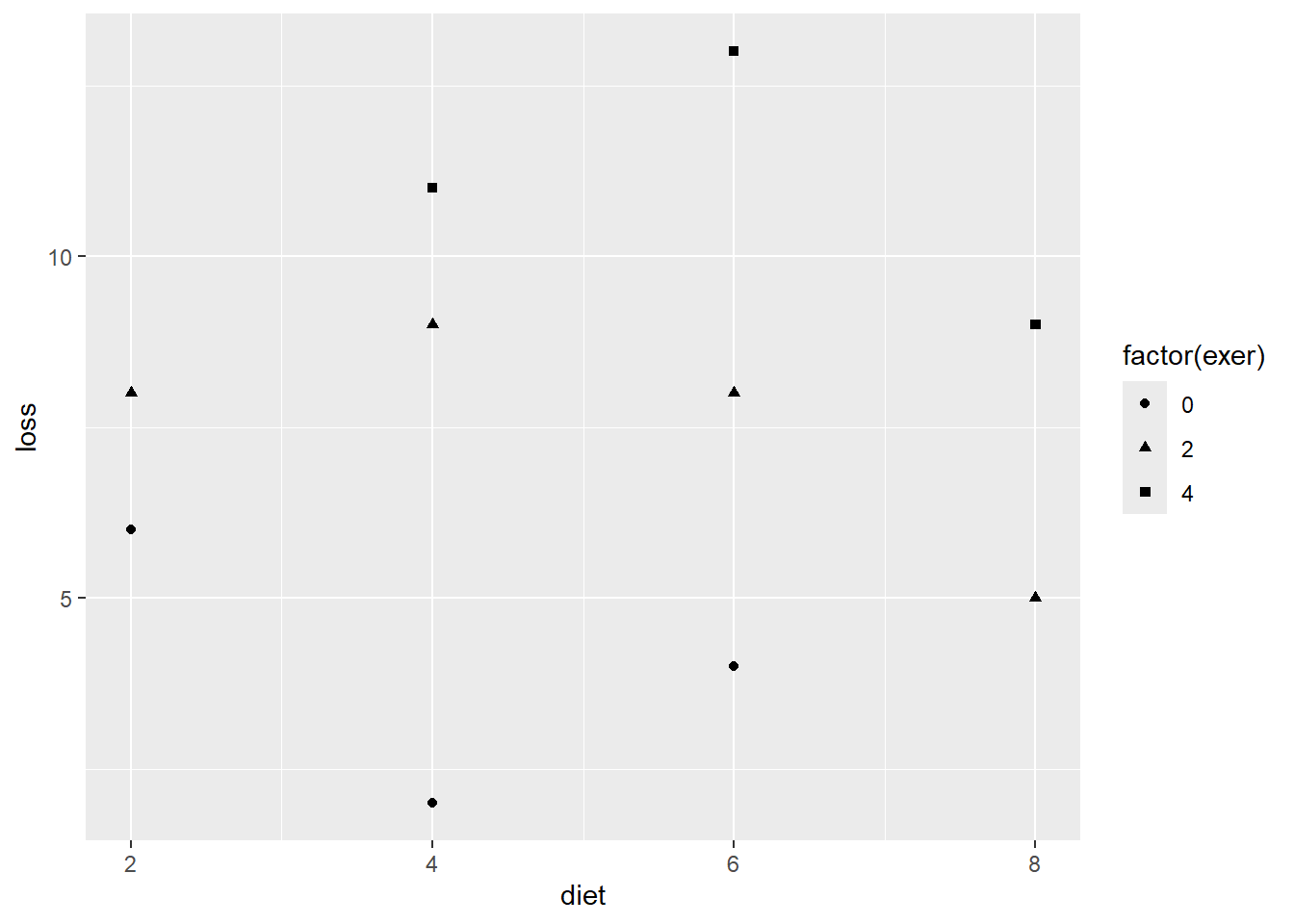
Figure 3.2
D&H Figure 3.1 (page 45) An example with positive simple association and negative partial association - BASIC

D&H Figure 3.1 (page 45) An example with positive simple association and negative partial association - BASIC 
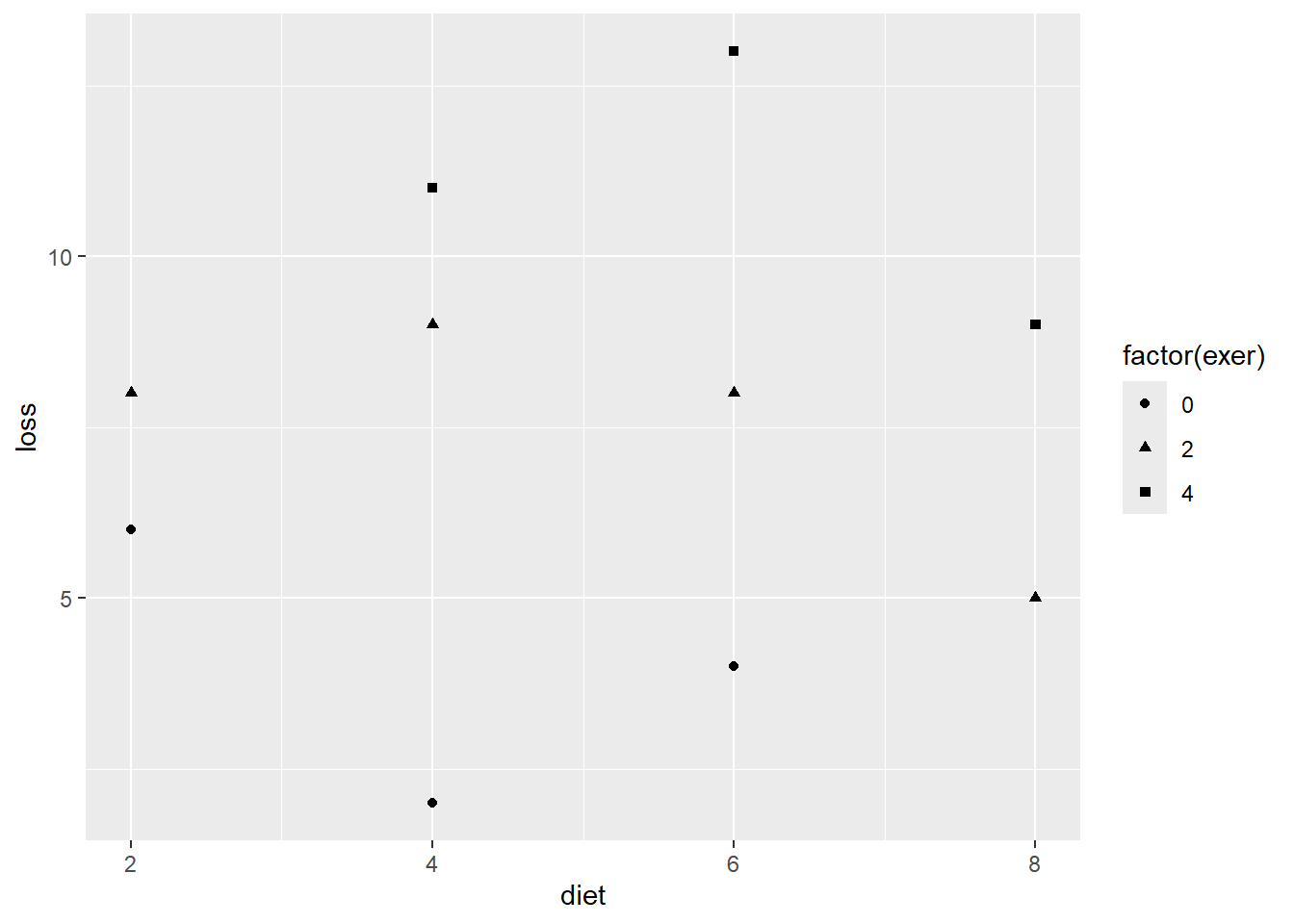
df_loss %>% 
  ggplot(aes(x = diet,
             y = loss)) +
  geom_point(aes(shape = factor(exer),
                 color = factor(exer)),
             size = 3)  +
  theme_bw() +
  labs(x = "Observed Food Intake)",
       y = "Observed Weight Loss",
       shape = "Exercise Frequency",
       color = "Exercise Frequency") +
  theme(legend.position = "bottom")

Figure 3.3
D&H Figure 3.1 (page 45) An example with positive simple association and negative partial association - BETTTER

D&H Figure 3.1 (page 45) An example with positive simple association and negative partial association - BETTTER 
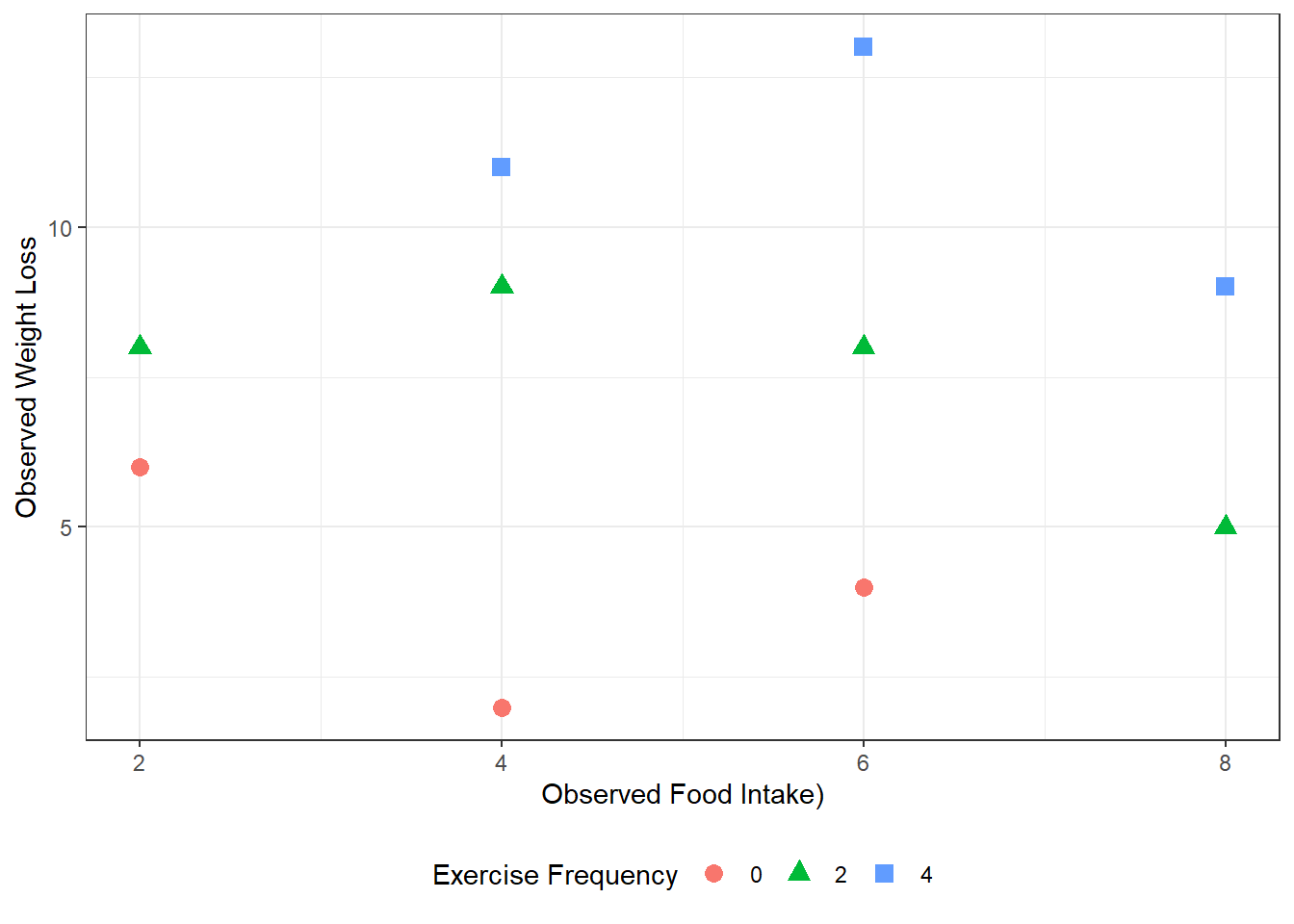
df_loss %>% 
  dplyr::mutate(exer = factor(exer)) %>% 
  ggplot(aes(x = diet,
             y = loss)) +
  geom_point(size = 3)  +
  theme_bw() +
  labs(x = "Observed Food Intake)",
       y = "Observed Weight Loss",
       shape = "Exercise Frequency",
       color = "Exercise Frequency") +
  theme(legend.position = "bottom") +
  geom_smooth(aes(group = 1),
              method = "lm",
              formula = y ~ x,
              se = FALSE)

Figure 3.4
D&H Figure 3.1 (page 45) An example with positive simple association and negative partial association - WORST

D&H Figure 3.1 (page 45) An example with positive simple association and negative partial association - WORST 
df_loss %>% 
  dplyr::mutate(exer = factor(exer)) %>% 
  ggplot(aes(x = diet,
             y = loss,
             group = exer)) +
  geom_point(aes(shape = exer,
                 color = exer),
             size = 3)  +
  theme_bw() +
  labs(x = "Observed Food Intake",
       y = "Observed Weight Loss",
       shape = "Exercise Frequency",
       color = "Exercise Frequency") +
  theme(legend.position = "bottom") +
  geom_smooth(aes(color = exer),
              method = "lm",
              formula = y ~ x,
              se = FALSE)

Figure 3.5
D&H Figure 3.1 (page 45) An example with positive simple association and negative partial association - BEST

D&H Figure 3.1 (page 45) An example with positive simple association and negative partial association - BEST

3.3 REGRESSION ANALYSIS

3.3.1 Fit the models

  • The dependent variable (DV) is weight loss (\(Y\))
  • The independent variables (IVs) are exercise and diet (\(X\))
fit_lm_exer <- lm(loss ~ exer,
                  data = df_loss)

fit_lm_diet <- lm(loss ~ diet,
                  data = df_loss)

fit_lm_both <- lm(loss ~ exer + diet,
                  data = df_loss)

fit_lm_three<- lm(loss ~ exer + diet + meta,
                  data = df_loss)

3.3.2 Equations

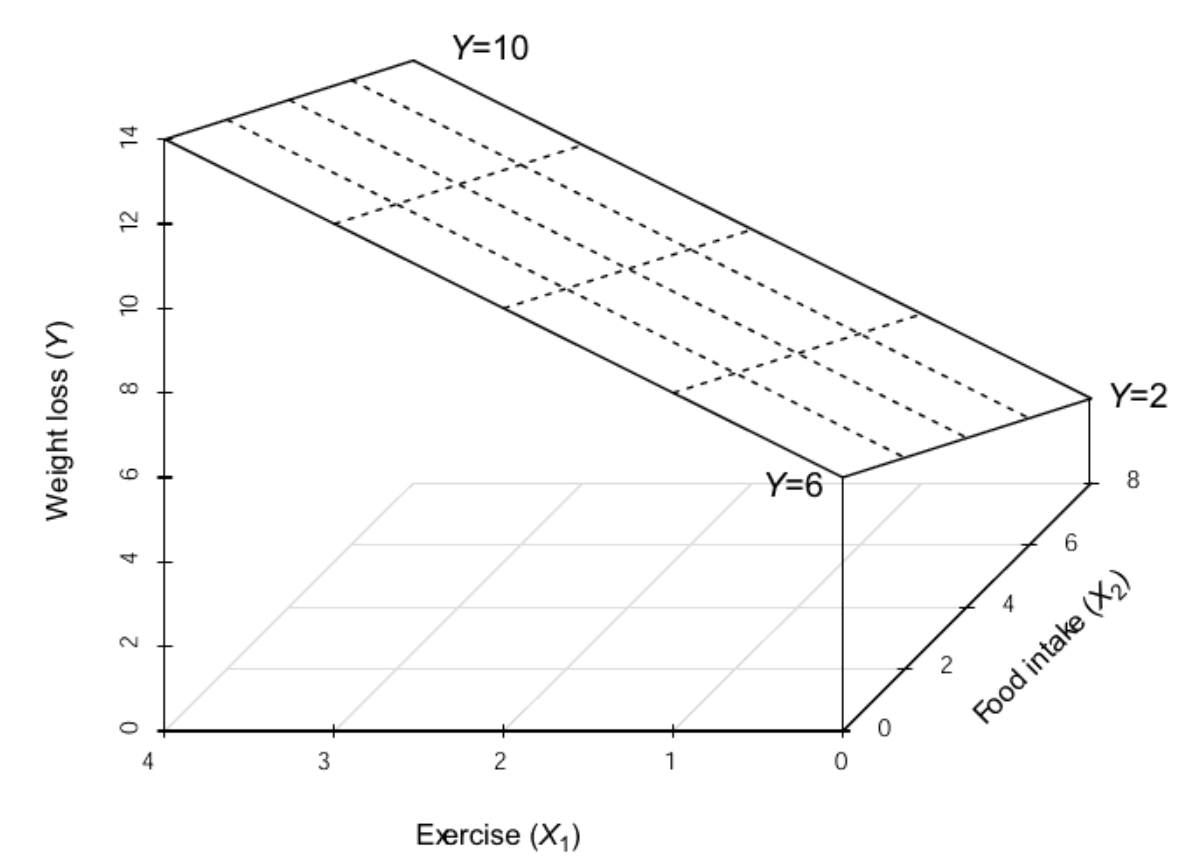
\[ \hat{loss} = 4 + 1.75(exercise) \\ \hat{loss} = 7.14 + 0.07(food) \\ \hat{loss} = 6 + 2(exercise) -0.5(food) \\ \hat{loss} = -1.636 + 1.045(exercise) -1.136(food) + 0.636(metabolism)\\ \]

3.3.3 Tables

apaSupp::tab_lms(list(fit_lm_exer, fit_lm_diet, fit_lm_both))
Table 3.4
Compare Regression Models

Model 1

Model 2

Model 3

Variable

b

(SE)

p

b

(SE)

p

b

(SE)

p

(Intercept)

4.00

(0.91)

.002**

7.14

(2.92)

.040*

6.00

(1.27)

.002**

exer

1.75

(0.36)

.001**

2.00

(0.33)

< .001***

diet

0.07

(0.54)

.898

-0.50

(0.25)

.088

AIC

43.54

57.23

41.08

BIC

44.45

58.14

42.29

R²

.746

.002

.838

Adjusted R²

.714

-.123

.791

Note.

* p < .05. ** p < .01. *** p < .001. 

apaSupp::tab_lms(list("Model 1\nExercise" = fit_lm_exer, 
                                 "Model 2\nFood Intake" = fit_lm_diet, 
                                 "Model 3\nBoth" = fit_lm_both),
                            var_labels = c("exer" = "Exercise",
                                           "diet" = "Food"),
                            narrow = TRUE,
                            docx = "DH_ch3_tab_lm3.docx",
                            caption = "Parameter Estimates for Weight Loss Regressed on Exercise Frequency and Food Intake",
                            general_note = "Dependent variable is average weekly weight lost in 100s of grams. Exercise is daily average hours and food intake is the average of 100's of calories above the recommendation. ")
Table 3.5
Parameter Estimates for Weight Loss Regressed on Exercise Frequency and Food Intake

Model 1
Exercise

Model 2
Food Intake

Model 3
Both

Variable

b

(SE)

b

(SE)

b

(SE)

(Intercept)

4.00

(0.91) **

7.14

(2.92) *

6.00

(1.27) **

Exercise

1.75

(0.36) **

2.00

(0.33) ***

Food

0.07

(0.54)

-0.50

(0.25)

AIC

43.54

57.23

41.08

BIC

44.45

58.14

42.29

R²

.746

.002

.838

Adjusted R²

.714

-.123

.791

Note. Dependent variable is average weekly weight lost in 100s of grams. Exercise is daily average hours and food intake is the average of 100's of calories above the recommendation.

* p < .05. ** p < .01. *** p < .001. 

apaSupp::tab_lms(list("Model 3\nTwo Predictors" = fit_lm_both, 
                      "Model 4\nThree Predictors" = fit_lm_three),
                 var_labels = c("exer" = "Exercise Freq",
                                "diet" = "Food Intake",
                                "meta" = "Metabolic Rate"),
                 caption = "Parameter Estimates for Weight Loss Regressed on Exercise Frequency, Food Intake, and Metabolic Rate",
                 general_note = "Dependent variable is average weekly weight lost in 100s of grams. Exercise is daily average hours and food intake is the average of 100's of calories above the recommendation. ")
Table 3.6
Parameter Estimates for Weight Loss Regressed on Exercise Frequency, Food Intake, and Metabolic Rate

Model 3
Two Predictors

Model 4
Three Predictors

Variable

b

(SE)

p

b

(SE)

p

(Intercept)

6.00

(1.27)

.002**

-1.64

(2.93)

.597

Exercise Freq

2.00

(0.33)

< .001***

1.05

(0.42)

.048*

Food Intake

-0.50

(0.25)

.088

-1.14

(0.29)

.008**

Metabolic Rate

0.64

(0.23)

.033*

AIC

41.08

34.94

BIC

42.29

36.45

R²

.838

.928

Adjusted R²

.791

.892

Note. Dependent variable is average weekly weight lost in 100s of grams. Exercise is daily average hours and food intake is the average of 100's of calories above the recommendation.

* p < .05. ** p < .01. *** p < .001.

3.3.4 Visualization

Figure 3.6
Darlington & Hayes: Figure 3.2, page 49

Darlington & Hayes: Figure 3.2, page 49 
interactions::interact_plot(model = fit_lm_both,
                            pred = diet,
                            modx = exer,
                            modx.values = 0:4) +
  theme_bw()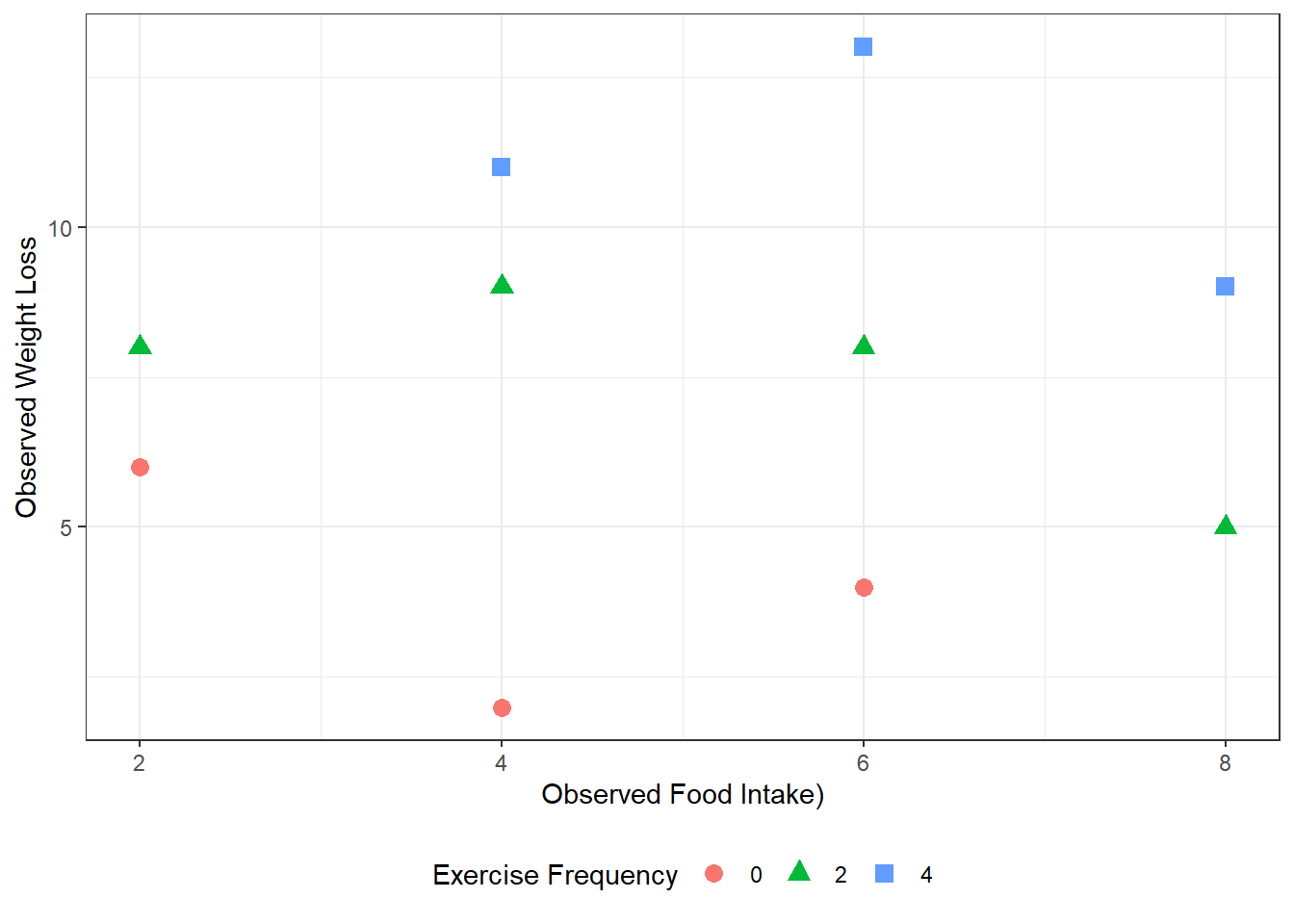 

interactions::interact_plot(model = fit_lm_both,
                            pred = exer,
                            modx = diet,
                            modx.values = c(0, 2, 4, 6, 8)) +
  theme_bw()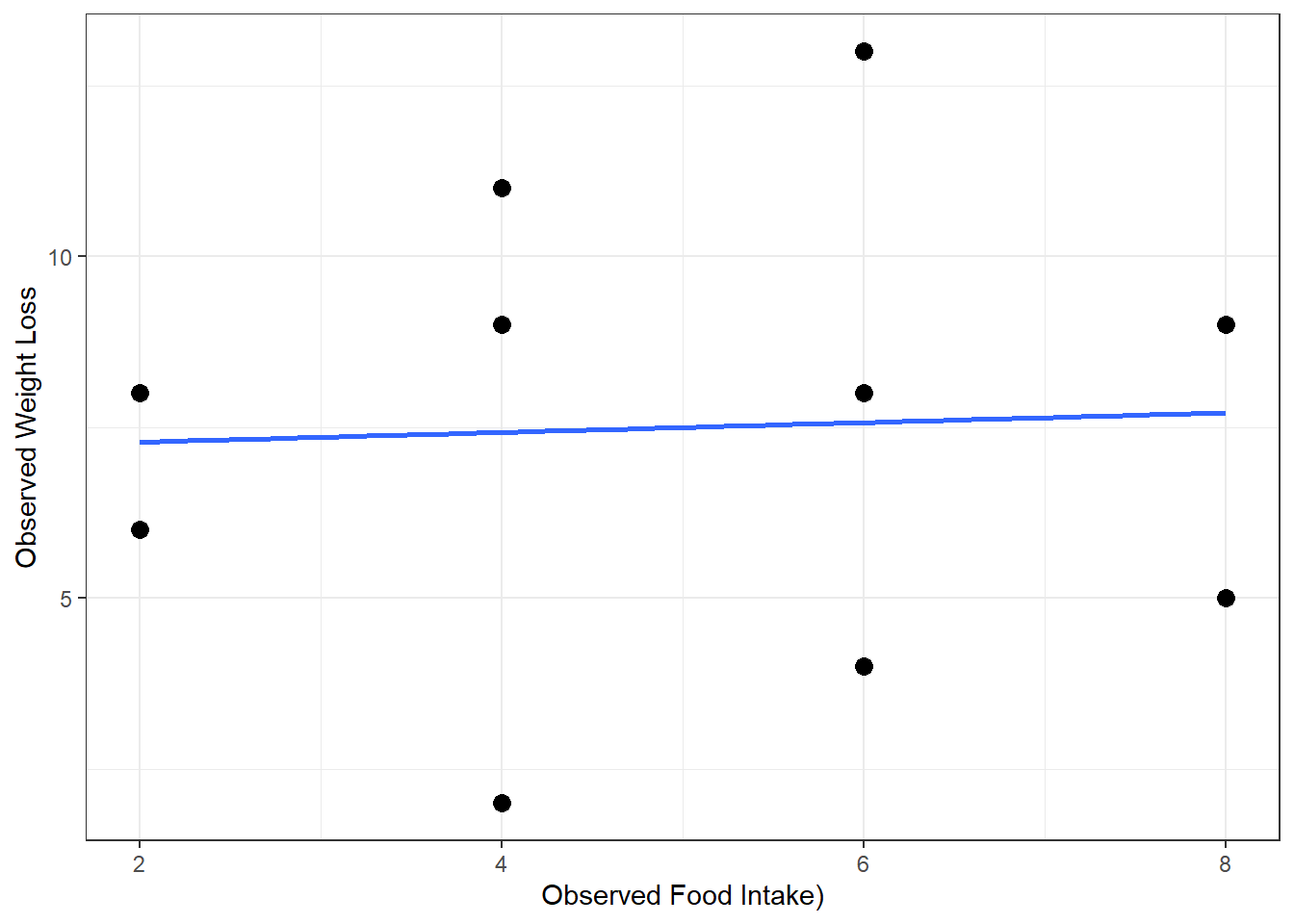 

interactions::interact_plot(model = fit_lm_three,
                            pred = exer,
                            modx = diet,
                            mod2 = meta,
                            modx.values = c(8, 5, 2),
                            modx.labels = c("1800 cal",
                                            "1500 cal",
                                            "1200 cal"),
                            mod2.values = c(16, 22.75),
                            mod2.labels = c("Low Metabolic Rate\n(Q1 = 16.00)", 
                                            "High Metabolic Rate\n(Q3 = 22.75)"),
                            x.label = "Daily Exercise, hours",
                            y.label = "Weight Loss, 100s grams/week",
                            legend.main = "Food Consumption") +
  theme_bw() +
  theme(legend.position = c(0, 1),
        legend.justification = c(-0.1, 1.1),
        legend.background = element_rect(color = "black"),
        legend.key.width = unit(2, "cm")) +
  scale_y_continuous(breaks = c(0, 5, 10, 15),
                     labels = c(0, 500, 1000, 1500))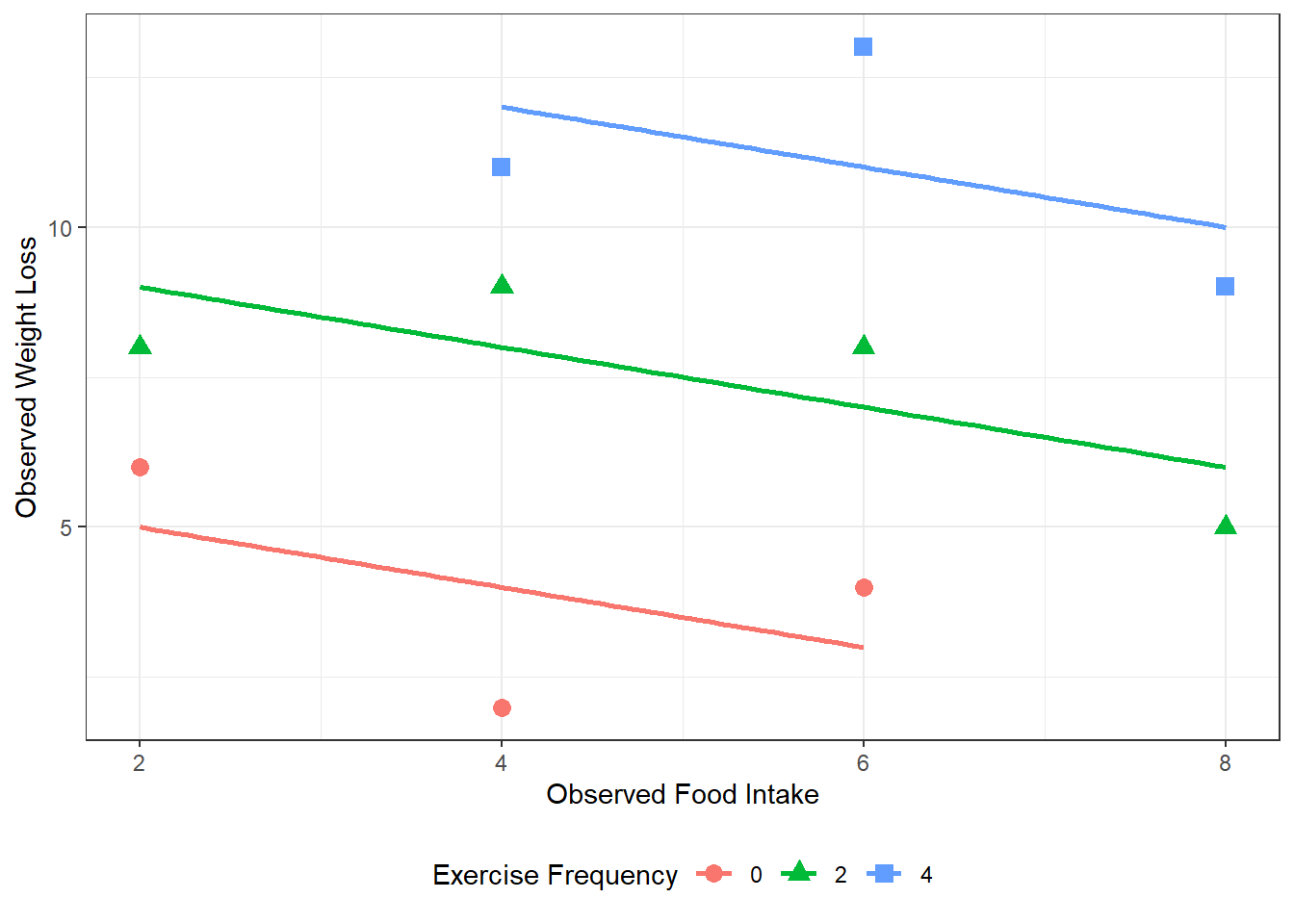

3.4 EFFECT SIZES

apaSupp::tab_lm(fit_lm_both,
                var_labels = c("exer" = "Exercise Freq",
                               "diet" = "Food Intake"),
                vif = TRUE,
                caption = "Parameter Estimates for Weight Loss Regressed on Exercise Frequency and Food Intake, with Effect Size Estimates",
                general_note = "Dependent variable is average weekly weight lost in 100s of grams. Exercise is daily average hours and food intake is the average of 100's of calories above the recommendation. ")
Table 3.7
Parameter Estimates for Weight Loss Regressed on Exercise Frequency and Food Intake, with Effect Size Estimates

b

(SE)

p

b∗b^*

VIF

η2\eta^2

ηp2\eta^2_p

(Intercept)

6.00

(1.27)

.002**

Exercise Freq

2.00

(0.33)

< .001***

0.99

1.17

.835

.837

Food Intake

-0.50

(0.25)

.088

-0.33

1.17

.091

.360

R²

.838

Adjusted R²

.791

Note. N = 10. b∗b^* = standardize coefficient; VIF = variance inflation factor; η2\eta^2 = semi-partial correlation; ηp2\eta^2_p = partial correlation; p = significance from Wald t-test for parameter estimate. Dependent variable is average weekly weight lost in 100s of grams. Exercise is daily average hours and food intake is the average of 100's of calories above the recommendation.

* p < .05. ** p < .01. *** p < .001. 

apaSupp::tab_lm(fit_lm_three,
                var_labels = c("exer" = "Exercise Freq",
                               "diet" = "Food Intake"),
                vif = TRUE,
                caption = "Parameter Estimates for Weight Loss Regressed on Exercise Frequency, Food Intake and Metabolic Rate, with Effect Size Estimates",
                general_note = "Dependent variable is average weekly weight lost in 100s of grams. Exercise is daily average hours and food intake is the average of 100's of calories above the recommendation. ")
Table 3.8
Parameter Estimates for Weight Loss Regressed on Exercise Frequency, Food Intake and Metabolic Rate, with Effect Size Estimates

b

(SE)

p

b∗b^*

VIF

η2\eta^2

ηp2\eta^2_p

(Intercept)

-1.64

(2.93)

.597

Exercise Freq

1.05

(0.42)

.048*

0.52

3.62

.074

.505

Food Intake

-1.14

(0.29)

.008**

-0.74

3.08

.179

.713

meta

0.64

(0.23)

.033*

0.80

7.00

.090

.557

R²

.928

Adjusted R²

.892

Note. N = 10. b∗b^* = standardize coefficient; VIF = variance inflation factor; η2\eta^2 = semi-partial correlation; ηp2\eta^2_p = partial correlation; p = significance from Wald t-test for parameter estimate. Dependent variable is average weekly weight lost in 100s of grams. Exercise is daily average hours and food intake is the average of 100's of calories above the recommendation.

* p < .05. ** p < .01. *** p < .001.

3.4.1 Semipartial Correlation

Unique contribution

effectsize::r2_semipartial(fit_lm_both)
# A tibble: 2 × 5
  Term  r2_semipartial    CI CI_low CI_high
  <chr>          <dbl> <dbl>  <dbl>   <dbl>
1 exer          0.835   0.95  0.675       1
2 diet          0.0914  0.95  0           1
effectsize::r2_semipartial(fit_lm_three)
# A tibble: 3 × 5
  Term  r2_semipartial    CI   CI_low CI_high
  <chr>          <dbl> <dbl>    <dbl>   <dbl>
1 exer          0.0735  0.95 0.000735       1
2 diet          0.179   0.95 0.00179        1
3 meta          0.0904  0.95 0.000904       1

3.4.2 Eta Squared

effectsize::eta_squared(fit_lm_both, partial = FALSE)
# A tibble: 2 × 5
  Parameter   Eta2    CI CI_low CI_high
  <chr>      <dbl> <dbl>  <dbl>   <dbl>
1 exer      0.746   0.95  0.336       1
2 diet      0.0914  0.95  0           1
effectsize::eta_squared(fit_lm_three, partial = FALSE)
# A tibble: 3 × 5
  Parameter   Eta2    CI CI_low CI_high
  <chr>      <dbl> <dbl>  <dbl>   <dbl>
1 exer      0.746   0.95  0.284       1
2 diet      0.0914  0.95  0           1
3 meta      0.0904  0.95  0           1
effectsize::eta_squared(fit_lm_both, partial = TRUE)
# A tibble: 2 × 5
  Parameter Eta2_partial    CI CI_low CI_high
  <chr>            <dbl> <dbl>  <dbl>   <dbl>
1 exer             0.821  0.95  0.494       1
2 diet             0.36   0.95  0           1
effectsize::eta_squared(fit_lm_three, partial = TRUE)
# A tibble: 3 × 5
  Parameter Eta2_partial    CI CI_low CI_high
  <chr>            <dbl> <dbl>  <dbl>   <dbl>
1 exer             0.912  0.95 0.699        1
2 diet             0.559  0.95 0.0445       1
3 meta             0.557  0.95 0.0425       1

3.4.3 Standardized Regression Coefficients

parameters::standardise_parameters(fit_lm_both)
# A tibble: 3 × 5
  Parameter   Std_Coefficient    CI CI_low CI_high
  <chr>                 <dbl> <dbl>  <dbl>   <dbl>
1 (Intercept)        8.24e-17  0.95 -0.342  0.342 
2 exer               9.87e- 1  0.95  0.598  1.38  
3 diet              -3.26e- 1  0.95 -0.716  0.0626
parameters::standardise_parameters(fit_lm_three)
# A tibble: 4 × 5
  Parameter   Std_Coefficient    CI   CI_low CI_high
  <chr>                 <dbl> <dbl>    <dbl>   <dbl>
1 (Intercept)        1.65e-16  0.95 -0.254     0.254
2 exer               5.16e- 1  0.95  0.00601   1.03 
3 diet              -7.42e- 1  0.95 -1.21     -0.272
4 meta               7.96e- 1  0.95  0.0866    1.50

3.4.4 Cohen’s \(f\) (see chapter 8)

Cohen’s \(f\) (Cohen, 1988) is appropriate for calculating the effect size within a multiple regression model in which the independent variable of interest and the dependent variable are both continuous.

effectsize::cohens_f_squared(fit_lm_both,
                             partial = TRUE)
# A tibble: 2 × 5
  Parameter Cohens_f2_partial    CI CI_low CI_high
  <chr>                 <dbl> <dbl>  <dbl>   <dbl>
1 exer                  4.59   0.95  0.976     Inf
2 diet                  0.563  0.95  0         Inf
effectsize::cohens_f_squared(fit_lm_both,
                             partial = FALSE)
# A tibble: 2 × 5
  Parameter Cohens_f2    CI CI_low CI_high
  <chr>         <dbl> <dbl>  <dbl>   <dbl>
1 exer          2.94   0.95  0.506     Inf
2 diet          0.101  0.95  0         Inf

3.5 VARIANCE INFLATION FACTORS

car::vif(fit_lm_both)
    exer     diet 
1.166667 1.166667 
car::vif(fit_lm_three)
    exer     diet     meta 
3.621212 3.075758 7.000000

3.6 CONCLUSION: SPECIFIC QUESTIONS

apaSupp::tab_lm(fit_lm_both, vif = TRUE)
Table 3.9
Parameter Estimates for Linear Regression

b

(SE)

p

b∗b^*

VIF

η2\eta^2

ηp2\eta^2_p

(Intercept)

6.00

(1.27)

.002**

exer

2.00

(0.33)

< .001***

0.99

1.17

.835

.837

diet

-0.50

(0.25)

.088

-0.33

1.17

.091

.360

R²

.838

Adjusted R²

.791

Note. N = 10. b∗b^* = standardize coefficient; VIF = variance inflation factor; η2\eta^2 = semi-partial correlation; ηp2\eta^2_p = partial correlation; p = significance from Wald t-test for parameter estimate.

* p < .05. ** p < .01. *** p < .001. 

confint(fit_lm_both)
                2.5 %     97.5 %
(Intercept)  2.985316 9.01468433
exer         1.211792 2.78820808
diet        -1.095829 0.09582931

\[ \hat{loss} = 6 + 2(exercise) -0.5(food) \]

Suppose an examination of the literature on diet, exercise, and weight loss led you to the following conclusions:

  1. People who eat the minimum number of calories to maintain good health and who do not exercise at all will lose how much?
fit_lm_both %>% 
  emmeans::emmeans(~ exer + diet,
                   at = list(exer = 0,
                             diet = 0))
 exer diet emmean   SE df lower.CL upper.CL
    0    0      6 1.27  7     2.99     9.01

Confidence level used: 0.95

The estimated marginal mean weight loss is 600 grams per week among thoes who eat the minimum number of calories to maintain good health and who do not exercise at, b = 6.00, 95% CI = [2.99, 9.01].

  1. If food intake is held constant, then each 1 hour of average daily exercise leads to how much more weight loss?
fit_lm_both %>% 
  emmeans::emmeans(~ exer + diet,
                   at = list(exer = 0:4))
 exer diet emmean    SE df lower.CL upper.CL
    0    5    3.5 0.820  7     1.56     5.44
    1    5    5.5 0.583  7     4.12     6.88
    2    5    7.5 0.478  7     6.37     8.63
    3    5    9.5 0.583  7     8.12    10.88
    4    5   11.5 0.820  7     9.56    13.44

Confidence level used: 0.95

Holding food consumption constant, each additional hour of daily exercise is associated with 200 grams additional weight lost per week, b = 2.00, 95% CI = [1.21, 2.79].

  1. If exercise is held constant, then each one unit of food intake per day (i.e., 100 calories) above the minimum to maintain good health translates to much weight gain?
fit_lm_both %>% 
  emmeans::emmeans(~ diet,
                   at = list(diet = 0:4))
 diet emmean    SE df lower.CL upper.CL
    0   10.0 1.350  7     6.81    13.19
    1    9.5 1.120  7     6.86    12.14
    2    9.0 0.894  7     6.89    11.11
    3    8.5 0.695  7     6.86    10.14
    4    8.0 0.540  7     6.72     9.28

Confidence level used: 0.95

Holding exercise constant, each additional 100 calories of food consumed daily is associated with 50 grams weight gained per week, b = -0.50, 95% CI = [1.21, 2.79].

  1. If a person exercises 2 hours per week and eats 600 more calories than the minimum, how much weight would they loose weekly on average?
fit_lm_both %>% 
  emmeans::emmeans(~ exer + diet,
                   at = list(exer = 2,
                             diet = 6))
 exer diet emmean   SE df lower.CL upper.CL
    2    6      7 0.54  7     5.72     8.28

Confidence level used: 0.95

On average, 700 grams were lost per week amonth participants who exrcised 2 hours a week and consumed 6,600 more calories, 95% CI [572, 828].