4 D&H Ch3b - Multiple Regression: “Sport Skill”

Compiled: October 15, 2025

Darlington & Hayes, Chapter 3’s second example

# install.packages("remotes")
# remotes::install_github("sarbearschwartz/apaSupp") # 9/17/2025

library(tidyverse)   
library(flextable)
library(apaSupp)       # not on CRAN, get from GitHub (above) 
library(GGally)    
library(ggpubr)  
library(interactions) 
library(effectsize)
library(performance)
library(ggResidpanel)

4.1 PURPOSE

4.1.1 Research Question

Are sports skills related to preference?

4.1.2 Data Description

4.1.2.1 Variables

Independent Variables (IV, \(X\)) * soft skill at softball * basket skill at basketball

Dependent Variable (DV, \(Y\)) * pref On a scale from 1 to 9, which sport do you prefer?” + 1 = much prefer softball + 5 = no preference + 9 = much prefer basketball

df_sport <- tibble::tribble(~id, ~soft, ~basket, ~pref,
                            1,   4, 17, 1,
                            2,  56, 60, 3,
                            3,  25,  3, 8,
                            4,  50, 52, 4,
                            5,   5, 16, 2,
                            6,  72, 84, 2,
                            7, 100, 95, 5,
                            8,  39, 20, 8,
                            9,  81, 75, 5,
                            10,  61, 47, 7)
df_sport %>% 
  dplyr::select("ID" = id,
                "Softball Skill" = soft,
                "Basketball Skill" = basket,
                "Preference Score" = pref) %>% 
  flextable::flextable() %>% 
  apaSupp::theme_apa(caption = "D&H TAble 3.5 (pg 78) Skill at Softball, Basketball, and Preference") %>% 
  flextable::colformat_double(digits = 0)
Table 4.1
D&H TAble 3.5 (pg 78) Skill at Softball, Basketball, and Preference

ID

Softball Skill

Basketball Skill

Preference Score

1

4

17

1

2

56

60

3

3

25

3

8

4

50

52

4

5

5

16

2

6

72

84

2

7

100

95

5

8

39

20

8

9

81

75

5

10

61

47

7

4.2 EXPLORATORY DATA ANALYSIS

4.2.1 Univariate Statistics

Center: mean and median Spread: standard deviation, range (max - min), interquartile range (Q3 - Q1)

df_sport %>% 
  dplyr::select("Softball Skill" = soft,
                "Basketball Skill" = basket,
                "Preference Score" = pref) %>%
  apaSupp::tab_desc(caption = "Summary Statistics")
Table 4.2
Summary Statistics

NA

M

SD

min

Q1

Mdn

Q3

max

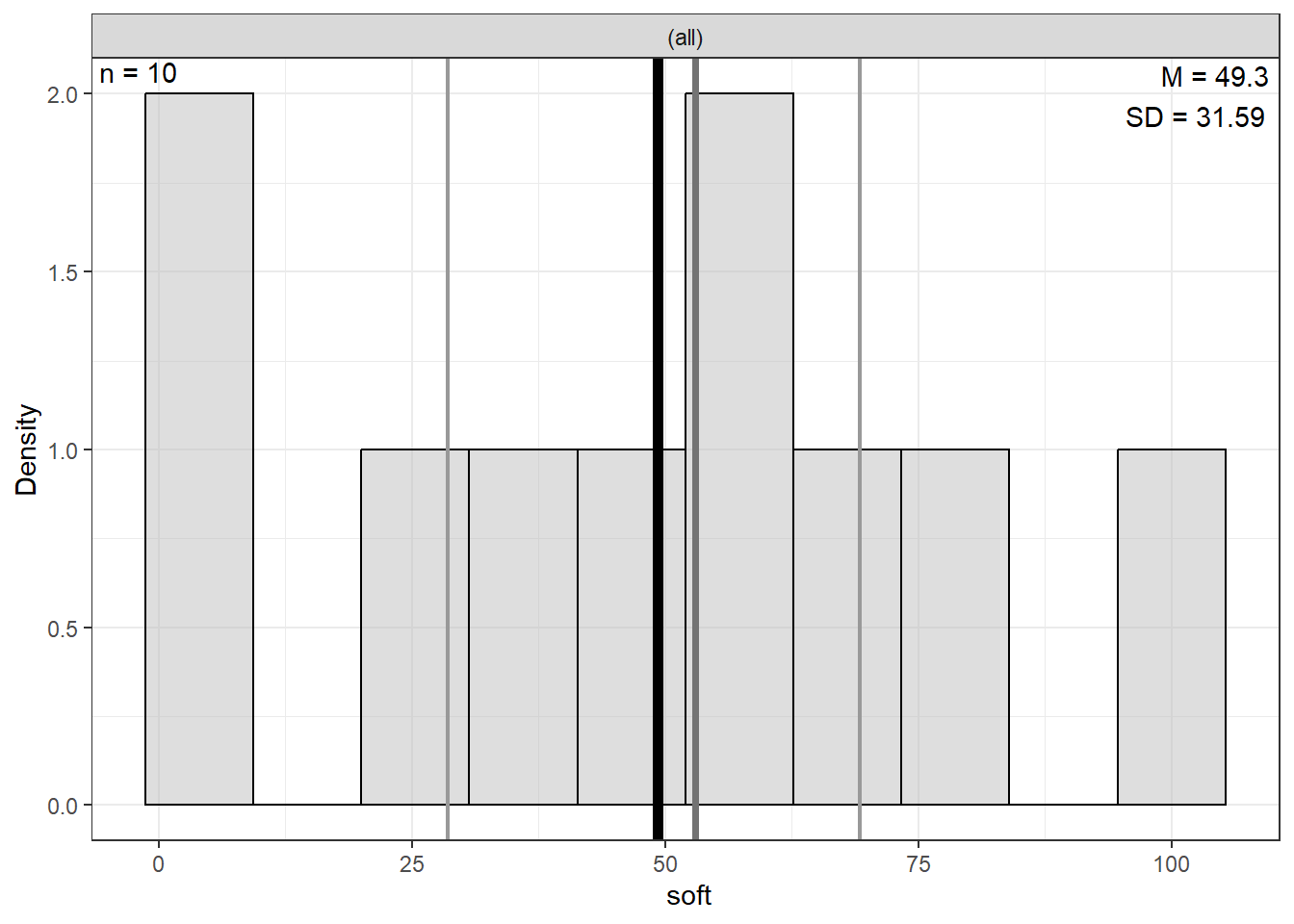
Softball Skill

0

49.30

31.59

4.00

28.50

53.00

69.25

100.00

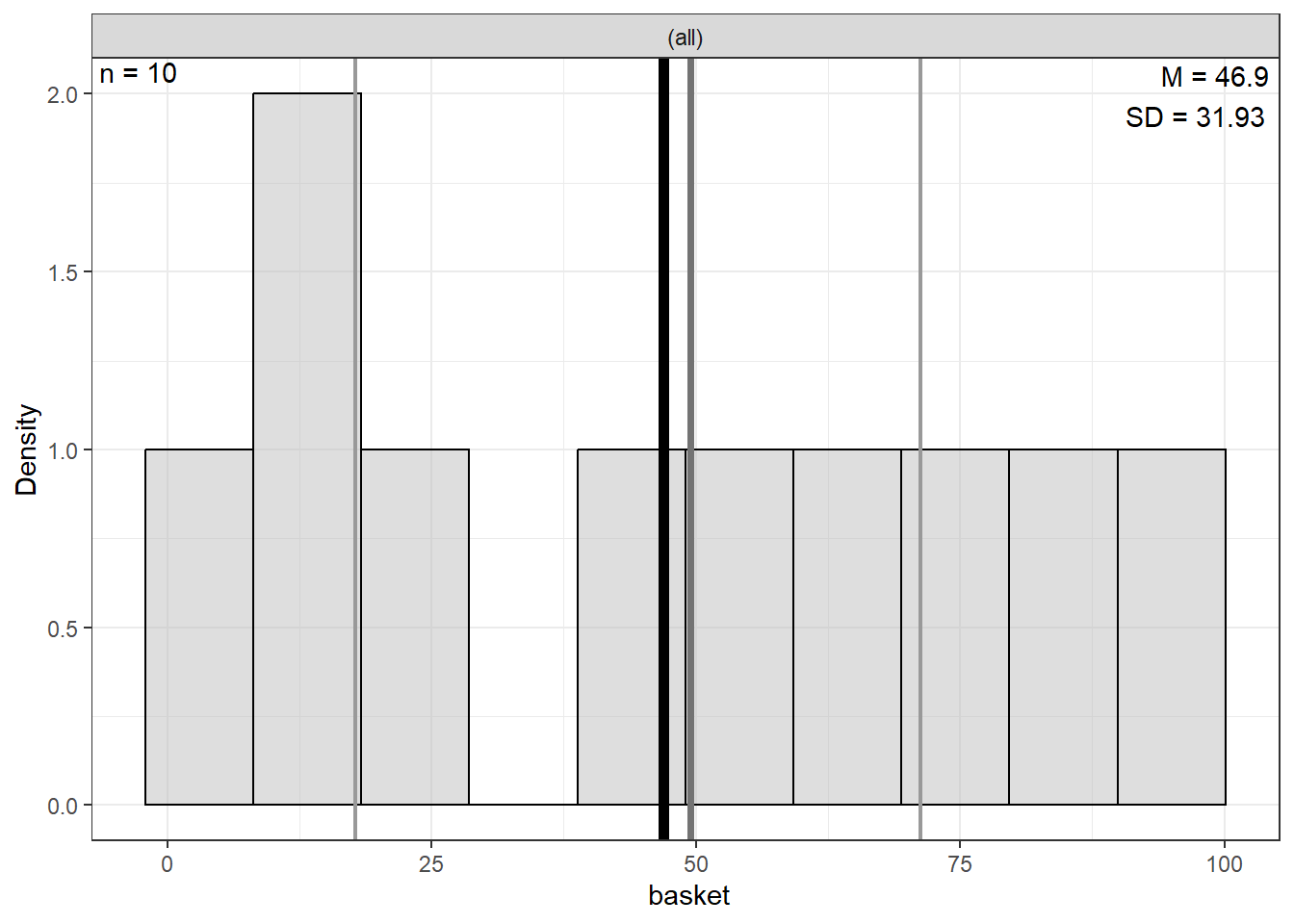
Basketball Skill

0

46.90

31.93

3.00

17.75

49.50

71.25

95.00

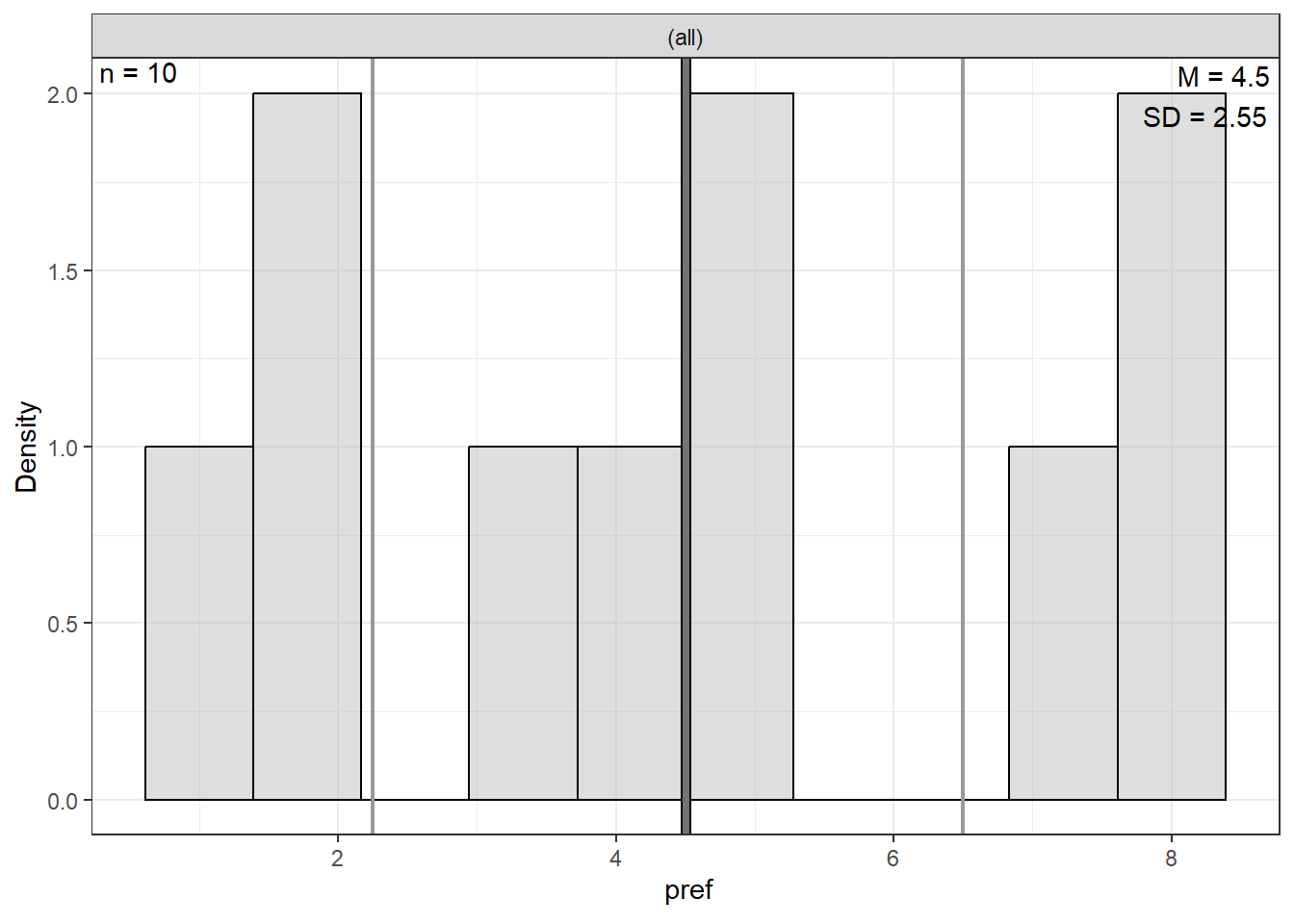
Preference Score

0

4.50

2.55

1.00

2.25

4.50

6.50

8.00

Note. N = 10. NA = not available or missing; Mdn = median; Q1 = 25th percentile; Q3 = 75th percentile.

4.2.2 Univariate Visualizations

df_sport %>% 
  apaSupp::spicy_histos(var = soft)

df_sport %>% 
  apaSupp::spicy_histos(var = basket)

df_sport %>% 
  apaSupp::spicy_histos(var = pref)

4.2.3 Bivariate Statistics

df_sport %>% 
  dplyr::select("Softball Skill" = soft,
                "Basketball Skill" = basket,
                "Preference Score" = pref) %>%
  apaSupp::tab_cor(caption = "Unadjusted, Pairwise Correlations")
Table 4.3
Unadjusted, Pairwise Correlations

Variable Pair

r

p

Softball Skill

Basketball Skill

.920

< .001***

Softball Skill

Preference Score

.210

.562

Basketball Skill

Preference Score

-.190

.590

Note. N = 10. r = Pearson's Product-Moment correlation coefficient.

* p < .05. ** p < .01. *** p < .001.

4.2.4 Bivariate Visualization

df_sport %>% 
  dplyr::select("Softball Skill" = soft,
                "Basketball Skill" = basket,
                "Preference Score" = pref) %>%
  data.frame %>% 
  GGally::ggscatmat() +
  theme_bw()

df_sport %>% 
  ggplot(aes(x = soft,        
             y = pref)) +   
  geom_point() +                    
  geom_smooth(method = "lm",
              formula = y ~ x) +
  ggpubr::stat_regline_equation(label.x = 75,
                                label.y = 1,
                                size = 6) +
  theme_bw() +
  labs(x = "Softball Skill",
       y = "Preference")

df_sport %>% 
  ggplot(aes(x = basket,        
             y = pref)) +   
  geom_point() +                    
  geom_smooth(method = "lm",
              formula = y ~ x) +
  ggpubr::stat_regline_equation(label.x = 75,
                                label.y = 1,
                                size = 6) +
  theme_bw() +
  labs(x = "Basketball Skill",
       y = "Preference")

4.3 REGRESSION ANALYSIS

  • The dependent variable (DV) is preference (\(Y\))
  • The independent variable (IVs) are skill levels (\(X\))

4.3.1 Fit the Models

fit_lm_soft <- lm(pref ~ soft,
                  data = df_sport)  

fit_lm_basket <- lm(pref ~ basket,
                    data = df_sport)

fit_lm_both <- lm(pref ~ soft + basket,
                  data = df_sport)
tab_lm3 <- apaSupp::tab_lms(list("Softball"   = fit_lm_soft, 
                                 "Basketball" = fit_lm_basket, 
                                 "Both"       = fit_lm_both),
                            var_labels = c("soft" = "Softball Skill",
                                           "basket" = "Basketball Skill"),
                            caption = "Parameter Estimates for Sport Preference Regression on Skill Level in Softball and Basketball",
                            general_note = "Dependent variable is preference rating on a scale of 1 (much prefer softball) to  9 (much prefer basketball).  Both softball and Baksetball skill levels are on a scale of 0 to 100.",
                            narrow = TRUE,
                            d = 3) 

tab_lm3
Table 4.4
Parameter Estimates for Sport Preference Regression on Skill Level in Softball and Basketball

Softball

Basketball

Both

Variable

b

(SE)

b

(SE)

b

(SE)

(Intercept)

3.669

(1.610)

5.228

(1.546) **

3.899

(0.200) ***

Softball Skill

0.017

(0.028)

0.198

(0.009) ***

Basketball Skill

-0.016

(0.028)

-0.195

(0.009) ***

AIC

51.597

51.658

10.495

BIC

52.504

52.565

11.706

R²

.0437

.0378

.9872

Adjusted R²

-.0759

-.0824

.9835

Note. Dependent variable is preference rating on a scale of 1 (much prefer softball) to 9 (much prefer basketball). Both softball and Baksetball skill levels are on a scale of 0 to 100.

* p < .05. ** p < .01. *** p < .001.

We call a set of regressors complementary if \(R^2\) for the set exceeds the sum of the individual values of \(r^2_{YX}\) . Thus, complementarity and collinearity are opposites, though either can occur only when regressors in a set are intercorrelated.

4.3.2 Visualize

interactions::interact_plot(model = fit_lm_both,
                            pred = soft,
                            modx = basket,
                            modx.values = c(25, 50, 75),
                            legend.main = "Basketball Skill\n(0-100)",
                            interval = TRUE) +
  theme_bw() +
  labs(x = "Softball Skill, (0-100)",
       y = "Estimated Marginal Mean Preference\n1 = much prefer softball\n9 = much prefer basketball") +
  coord_cartesian(ylim = c(1, 9)) +
  scale_y_continuous(breaks = 1:9) +
  theme(legend.position = c(0, 1),
        legend.justification = c(-.1, 1.1),
        legend.background = element_rect(color = "black"),
        legend.key.width = unit(1.5, "cm"))

4.3.3 Semipartial Correlation

apaSupp::tab_lm(fit_lm_both)
Table 4.5
Parameter Estimates for Linear Regression

b

(SE)

p

b∗b^*

η2\eta^2

ηp2\eta^2_p

(Intercept)

3.90

(0.20)

< .001***

soft

0.20

(0.01)

< .001***

2.45

.949

.987

basket

-0.20

(0.01)

< .001***

-2.44

.943

.987

R²

.987

Adjusted R²

.983

Note. N = 10. b∗b^* = standardize coefficient; η2\eta^2 = semi-partial correlation; ηp2\eta^2_p = partial correlation; p = significance from Wald t-test for parameter estimate.

* p < .05. ** p < .01. *** p < .001. 

apaSupp::tab_lm(fit_lm_both)
Table 4.6
Parameter Estimates for Linear Regression

b

(SE)

p

b∗b^*

η2\eta^2

ηp2\eta^2_p

(Intercept)

3.90

(0.20)

< .001***

soft

0.20

(0.01)

< .001***

2.45

.949

.987

basket

-0.20

(0.01)

< .001***

-2.44

.943

.987

R²

.987

Adjusted R²

.983

Note. N = 10. b∗b^* = standardize coefficient; η2\eta^2 = semi-partial correlation; ηp2\eta^2_p = partial correlation; p = significance from Wald t-test for parameter estimate.

* p < .05. ** p < .01. *** p < .001. 

effectsize::r2_semipartial(fit_lm_both)
# A tibble: 2 × 5
  Term   r2_semipartial    CI CI_low CI_high
  <chr>           <dbl> <dbl>  <dbl>   <dbl>
1 soft            0.949  0.95  0.756       1
2 basket          0.943  0.95  0.737       1

4.3.4 Venn Diagram - Variances

https://freetools.touchpoint.com/venn-diagram-template-generator

ABCD <- var(df_sport$pref)
ABCD
[1] 6.5
AB <- var(fit_lm_soft$residuals)
AB
[1] 6.216137
BC <- var(fit_lm_basket$residuals)
BC
[1] 6.254138
D <- var(fit_lm_both$residuals)
D
[1] 0.08349447
ABC <- ABCD - D
ABC
[1] 6.416506
A <- ABC - BC
A
[1] 0.1623674
C <- ABC - AB
C
[1] 0.2003681
B <- AB + BC - ABC
B
[1] 6.05377

4.3.5 Venn Diagram - Proportions

Total Variance in Preference Explained by Both Skills

R2 <- ABC/ABCD
R2
[1] 0.9871547

Variance in Preference Uniquely Explained by Softball skills, across all Basketball skill levels

sr2_soft <- A/ABCD
sr2_soft
[1] 0.0249796

Variance in Preference Uniquely Explained by Basketball skills, across all Softball skill levels

sr2_basket <- C/ABCD
sr2_basket
[1] 0.03082587

Variance in Preference Explained by Softball skills, when holding Basketball skill constant

pr2_soft <- A/(A + D)
pr2_soft
[1] 0.6604009
pr2_basket <- C/(C + D)
pr2_basket
[1] 0.7058631

4.3.6 Residual Diagnostics

performance::check_residuals(fit_lm_both)
OK: Simulated residuals appear as uniformly distributed (p = 0.676).
ggResidpanel::resid_panel(fit_lm_both)