19 Ex: Count - GSS (Hoffman)

Compiled: October 15, 2025

19.1 PREPARATION

19.1.1 Load Packages

# install.packages("remotes")
# remotes::install_github("sarbearschwartz/apaSupp") # 9/17/2025
# remotes::install_github("sarbearschwartz/texreghelpr") 

library(haven)
library(tidyverse)   
library(flextable)
library(apaSupp)       # not on CRAN, get from GitHub (above) 
library(emmeans)
library(ggeffects)
library(psych)
library(interactions)
library(ggeffects)
library(effects)
library(MASS)
library(texreg)
library(performance)
library(pscl)

library(texreg)
library(texreghelpr)

19.1.2 Load Data

This dataset comes from John Hoffman’s textbook: Regression Models for Categorical, Count, and Related Variables: An Applied Approach (2004) Amazon link, 2014 edition

df_gss <- haven::read_spss("https://raw.githubusercontent.com/CEHS-research/data/master/Hoffmann_datasets/gss.sav") %>% 
  haven::as_factor() %>% 
  haven::zap_label() %>%    # remove SPSS junk
  haven::zap_formats() %>%  # remove SPSS junk
  haven::zap_widths() %>%   # remove SPSS junk 
  dplyr::mutate_if(is.factor, ~forcats::fct_relabel(.x, stringr::str_to_title))

str(df_gss)

tibble [2,903 × 20] (S3: tbl_df/tbl/data.frame)
 $ id      : num [1:2903] 402 1473 1909 334 1751 ...
 $ marital : Factor w/ 5 levels "Married","Widowed",..: 3 2 2 2 1 3 5 1 5 2 ...
 $ divorce : Factor w/ 2 levels "Yes","No": 1 2 2 1 2 1 2 1 2 2 ...
 $ childs  : Factor w/ 9 levels "0","1","2","3",..: 3 1 8 3 3 1 3 4 1 3 ...
 $ age     : num [1:2903] 54 24 75 41 37 40 36 33 18 35 ...
 $ income  : num [1:2903] 10 2 NA NA 12 NA 9 NA NA 6 ...
 $ polviews: Factor w/ 7 levels "Extreme Liberal",..: 4 5 7 4 7 7 NA 4 4 4 ...
 $ fund    : Factor w/ 3 levels "Fundamentalist",..: NA NA NA NA NA NA NA NA NA NA ...
 $ attend  : Factor w/ 9 levels "Never","Less Than Once A Year",..: NA NA NA NA NA NA 7 4 3 4 ...
 $ spanking: Factor w/ 4 levels "Strongly Agree",..: NA NA NA NA NA NA NA NA NA NA ...
 $ totrelig: num [1:2903] NA NA NA NA NA NA NA 1000 NA NA ...
 $ sei     : num [1:2903] 38.9 29 29.1 29 38.1 ...
 $ pasei   : num [1:2903] NA 48.6 22.5 26.7 38.1 ...
 $ volteer : num [1:2903] 0 0 0 1 1 0 0 0 1 0 ...
 $ female  : Factor w/ 2 levels "Male","Female": 2 1 2 2 1 2 2 2 2 1 ...
 $ nonwhite: Factor w/ 2 levels "White","Non-White": 2 1 2 1 1 1 2 1 2 1 ...
 $ prayer  : Factor w/ 6 levels "Never","Less Than Once A Week",..: 5 4 5 4 4 4 5 4 4 4 ...
 $ educate : num [1:2903] 12 17 8 12 12 NA 15 12 11 14 ...
 $ volrelig: Factor w/ 2 levels "No","Yes": 1 1 1 2 2 1 1 1 1 1 ...
 $ polview1: Factor w/ 3 levels "Liberal","Moderate",..: 2 3 3 2 3 3 NA 2 2 2 ...

df_gss %>% 
  dplyr::select(volteer, female, nonwhite, educate, income) %>% 
  tibble::glimpse()

Rows: 2,903
Columns: 5
$ volteer  <dbl> 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0…
$ female   <fct> Female, Male, Female, Female, Male, Female, Female, Female, F…
$ nonwhite <fct> Non-White, White, Non-White, White, White, White, Non-White, …
$ educate  <dbl> 12, 17, 8, 12, 12, NA, 15, 12, 11, 14, 14, 12, 20, 12, 15, 20…
$ income   <dbl> 10, 2, NA, NA, 12, NA, 9, NA, NA, 6, 12, 11, 12, 10, 12, 12, …

19.2 EXPLORATORY DATA ANALYSIS

apaSupp::spicy_histos(df_gss, var = educate, split = female)

apaSupp::spicy_histos(df_gss, var = income, split = female)

19.2.1 Entire Sample

df_gss %>%
  dplyr::select(volteer) %>% 
  apaSupp::tab1()

**Table 19.1**
Summary of Variables
	N = 2,903
volteer
0	2,376 (81.8%)
1	286 (9.9%)
2	133 (4.6%)
3	64 (2.2%)
4	19 (0.7%)
5	11 (0.4%)
6	7 (0.2%)
7	6 (0.2%)
9	1 (0.0%)
Note. Continuous variables are summarized with means (SD). Categorical variables are summarized with counts (%).

df_gss %>% 
  ggplot(aes(volteer)) +
  geom_bar(color = "black", alpha = .4)  +
  theme_bw() +
  labs(x = "Number of Volunteer Activities in the Past Year",
       y = "Frequency") +
  scale_x_continuous(breaks = seq(from = 0, to = 10, by = 1))

Figure 19.1
Hoffman Figure 6.3

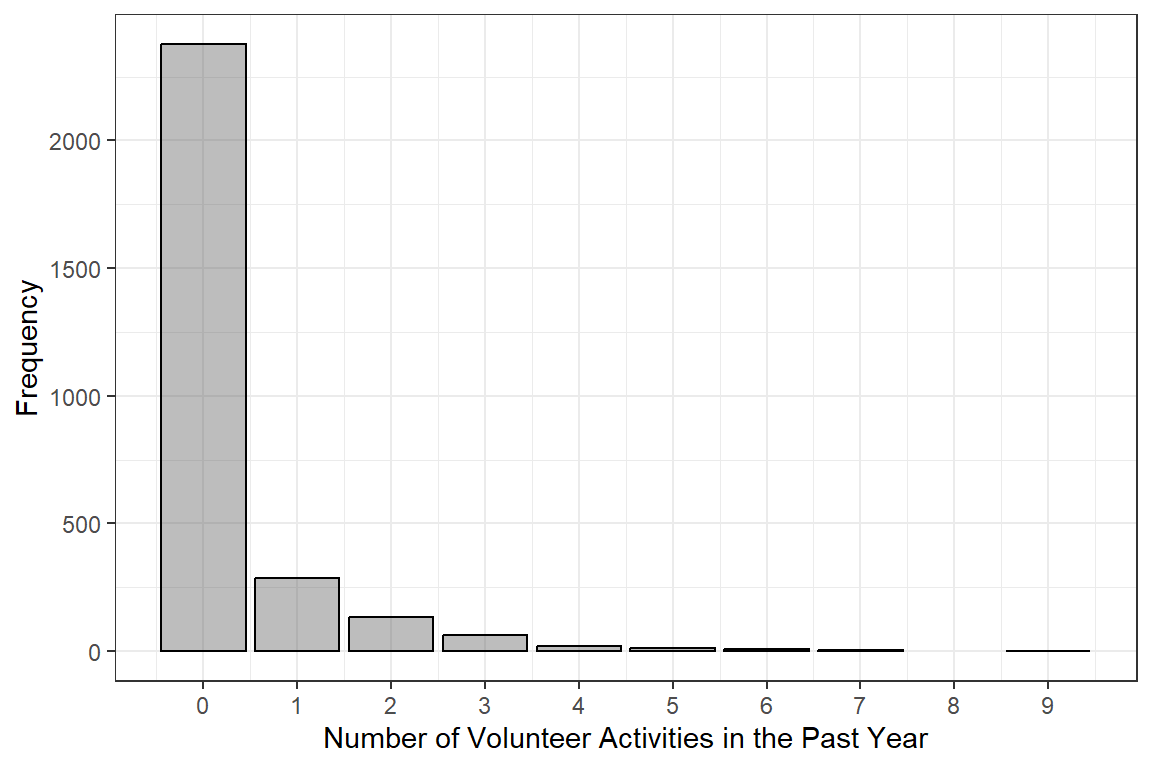
Interpretation:

The self-reported number of times each person volunteered in the past year is a count (0, 1, 2, …) that does NOT follow the normal distribution.

19.2.2 By Sex

df_gss %>% 
  dplyr::select(female, 
                "Volunteer" = volteer) %>% 
  apaSupp::tab1(split = "female")

**Table 19.2**
Summary of Variables
	Total N = 2903	Male n = 1285 (44.3%)	Female n = 1618 (55.7%)	p-value
Volunteer				.363
0	2,376 (81.8%)	1,057 (82.3%)	1,319 (81.5%)
1	286 (9.9%)	132 (10.3%)	154 (9.5%)
2	133 (4.6%)	50 (3.9%)	83 (5.1%)
3	64 (2.2%)	26 (2.0%)	38 (2.3%)
4	19 (0.7%)	10 (0.8%)	9 (0.6%)
5	11 (0.4%)	4 (0.3%)	7 (0.4%)
6	7 (0.2%)	5 (0.4%)	2 (0.1%)
7	6 (0.2%)	1 (0.1%)	5 (0.3%)
9	1 (0.0%)	0 (0.0%)	1 (0.1%)
Note. Continuous variables are summarized with means (SD) and significant group differences assessed via independent t-tests. Categorical variables are summarized with counts (%) and significant group differences assessed via Chi-squared tests for independence.
* p < .05. p < .01. * p < .001.

df_gss %>% 
  dplyr::select(female, 
                "Volunteer" = volteer) %>% 
  apaSupp::tab1(split = "female",
                type = list("Volunteer" = "continuous"),
                d = 3)

**Table 19.3**
Summary of Variables
	Total N = 2903	Male n = 1285 (44.3%)	Female n = 1618 (55.7%)	p-value
Volunteer	0.333 (0.886)	0.317 (0.849)	0.347 (0.914)	.3609
Note. Continuous variables are summarized with means (SD) and significant group differences assessed via independent t-tests. Categorical variables are summarized with counts (%) and significant group differences assessed via Chi-squared tests for independence.
* p < .05. p < .01. * p < .001.

df_gss %>% 
  t.test(volteer ~ female,
         data = .,
         var.equal = TRUE) # pooled variance assumes HOV


    Two Sample t-test

data:  volteer by female
t = -0.90608, df = 2901, p-value = 0.365
alternative hypothesis: true difference in means between group Male and group Female is not equal to 0
95 percent confidence interval:
 -0.09489802  0.03491235
sample estimates:
  mean in group Male mean in group Female 
           0.3167315            0.3467244

Interpretation:

Even though there are more women (n = 1818, 56%), the woman do report volunteering more over the past year (M = 0.35 vs. 0.32 time a year). This difference is NOT statistically significant when tested with an independent groups t-test, p = .365. The t-test does treat the volunteering variable as if it were normally distributed, which is not the case.

df_gss %>% 
  dplyr::select(volteer) %>% 
  dplyr::summarise_all(list(mean = mean, 
                            var = var))

# A tibble: 1 × 2
   mean   var
  <dbl> <dbl>
1 0.333 0.785

Interpretation:

The number of self-reported volunteer activities is a count, but it is more dispersed that the Poisson distribution would expect. The over-dispersion is evident in that the variance (0.78) is much larger than the mean (0.33). This suggests that the Negative Binomial distribution may fit the data better than a Poisson distribution.

DV: Count Scale

df_gss %>% 
  ggplot(aes(x = female,
             y = volteer)) +
  geom_violin(aes(fill = female), alpha = .4)  +
  stat_summary(fun = mean, geom = "crossbar", color = "red") +
  theme_bw() +
  labs(y = "Number of\nVolunteer Activities in the Past Year",
       x = NULL) +
  scale_y_continuous(breaks = seq(from = 0, to = 10, by = 2)) +
  scale_fill_manual(values = c("dodgerblue", "coral3"))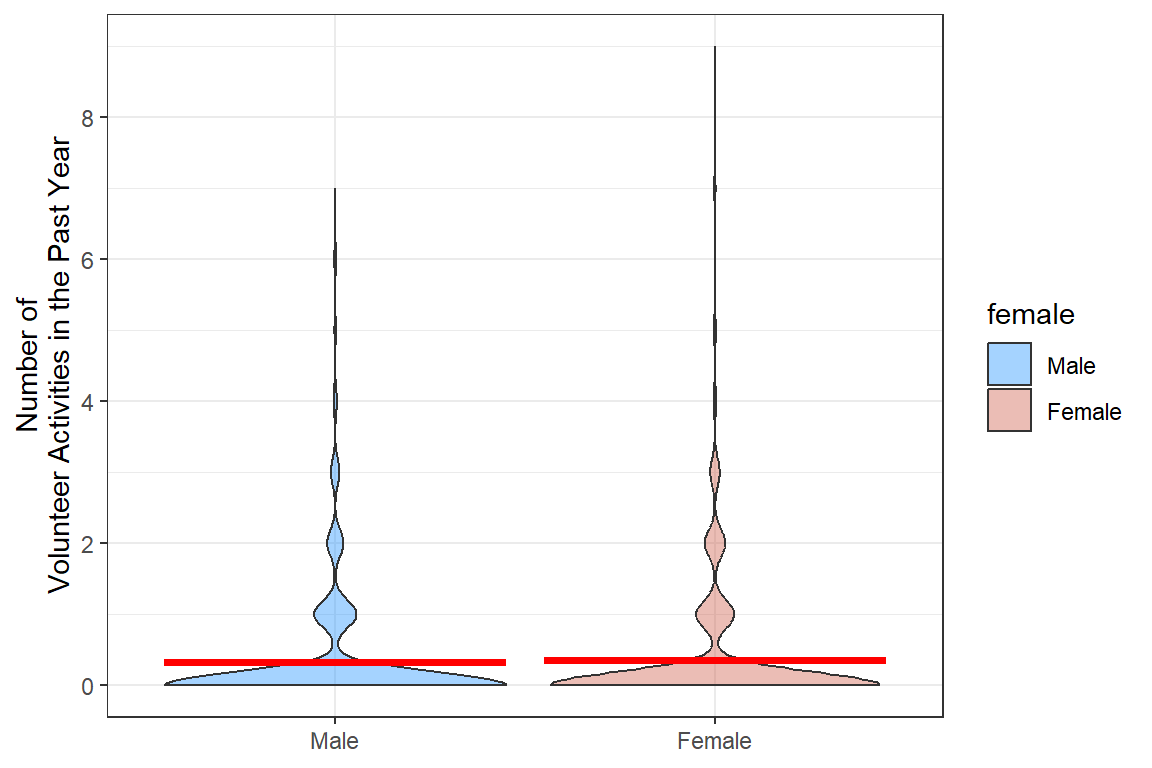

DV: Log of the Count Scale (plus a tiny amount)

df_gss %>% 
  dplyr::mutate(volteer_log = log(volteer + 0.01)) %>% 
  ggplot(aes(x = female,
             y = volteer_log)) +
  geom_violin(aes(fill = female), alpha = .4)  +
  stat_summary(fun = mean, geom = "crossbar", color = "red") +
  theme_bw() +
  labs(y = "Log of 0.01 + Number of\nVolunteer Activities in the Past Year",
       x = NULL) +
  scale_fill_manual(values = c("dodgerblue", "coral3"))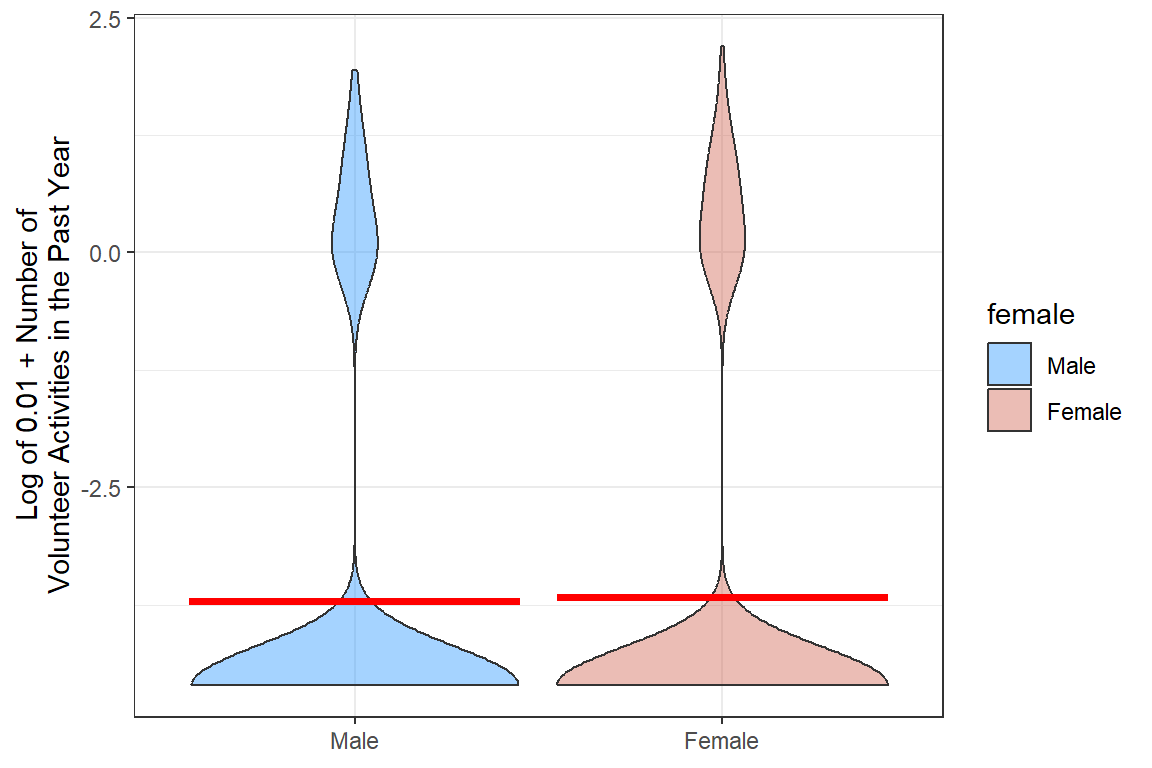

19.3 SIMPLE POISSON REGRESSION

Only use the single predictor: female

The simple model will give us the “Unadjusted” rates.

19.3.1 Fit the model

glm_possion_1 <- glm(volteer ~ female,
                     data = df_gss,
                     family = poisson(link = "log"))

summary(glm_possion_1)


Call:
glm(formula = volteer ~ female, family = poisson(link = "log"), 
    data = df_gss)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -1.14970    0.04957  -23.19   <2e-16 ***
femaleFemale  0.09048    0.06511    1.39    0.165    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 3658.1  on 2902  degrees of freedom
Residual deviance: 3656.2  on 2901  degrees of freedom
AIC: 4924.1

Number of Fisher Scoring iterations: 6

Interpretation:

The intercept is the predicted log(count) when all the predictors are equal to zero (or the reference category for factors). Since the only predictor in this model is female, the IRR = -1.15 is for males and is statistically significant, p < .001.

The parameter estimate for the categorical predictor female capture how different the log(count) is for female, compared to males. This is not statistically significant, p = .165.

Thus far, there is no evidence that males and females volunteer more or less, on average (marginally).

Note: The deviance residuals range as high as 6.47!!! That is quite high for a z-score.

19.3.2 Parameter Estimates

family(glm_possion_1)


Family: poisson 
Link function: log

19.3.2.1 Link Scale

Coefficients are in terms of the LOG of the number of times a person volunteers per year, or log(IRR).

glm_possion_1 %>% coef()

 (Intercept) femaleFemale 
 -1.14970081   0.09047562

19.3.2.2 Count Scale

Exponentiation of the coefficients (betas) returns the values to the original scale (number of times a person volunteers per year) and is referred to as the incident rate ratio (IRR).

glm_possion_1 %>% coef() %>% exp()

 (Intercept) femaleFemale 
   0.3167315    1.0946948

apaSupp::tab_glm(glm_possion_1)

**Table 19.4**
Parameter Estimates for Generalized Linear Regression
	Incident Rate Ratio		Log Scale
Variable	IRR	95% CI	b	(SE)	p
(Intercept)	0.32	[0.29, 0.35]	-1.15	(0.05)	< .001***
female
Male	—	—	—	—
Female	1.09	[0.96, 1.24]	.1	(0.07)	.165
pseudo-R²	< .001
Note. N = 2903. CI = confidence interval. Significance denotes Wald t-tests for parameter estimates. Coefficient of determination displays Nagelkerke's pseudo-R².
* p < .05. p < .01. * p < .001.

19.3.3 Predictions

19.3.3.1 Link Scale

Note: Results are given on the log (not the response) scale

glm_possion_1 %>% 
  emmeans::emmeans(~ female)

 female emmean     SE  df asymp.LCL asymp.UCL
 Male    -1.15 0.0496 Inf     -1.25    -1.053
 Female  -1.06 0.0422 Inf     -1.14    -0.976

Results are given on the log (not the response) scale. 
Confidence level used: 0.95

Interpretation:

Males have a lower log(count) than females, but this difference is not significant due to the good deal of overlap in the confidence intervals.

19.3.3.2 Count Scale:

Note: These means are on the original scale (number of volunteer activities in the past year).

These standard errors ARE the so-called “delta-method standard errors” that Stat gives.

glm_possion_1 %>% 
  emmeans::emmeans(~ female,
                   type = "response")

 female  rate     SE  df asymp.LCL asymp.UCL
 Male   0.317 0.0157 Inf     0.287     0.349
 Female 0.347 0.0146 Inf     0.319     0.377

Confidence level used: 0.95 
Intervals are back-transformed from the log scale

These standard errors are NOT the so-called “delta-method standard errors” that Stat gives.

# Hoffmann Example 6.4 (continued...)
ggeffects::ggemmeans(model = glm_possion_1,
                     terms = c("female")) %>% 
  data.frame()

# A tibble: 2 × 6
  x      predicted std.error conf.low conf.high group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <fct>
1 Male       0.317    0.0496    0.287     0.349 1    
2 Female     0.347    0.0422    0.319     0.377 1

0.3467 / 0.3167

[1] 1.094727

Interpretation:

The marginal count/year or rate is: * 0.32 times/year for males * 0.35 times/year for females

The incident rate ratio (IRR) is: * 9% more times higher, for females compared to males

19.4 MULTIPLE POISSON REGRESSION

Only using multiple predictors: female, nonwhite, educate, and income

The more compled model will give us the “Adjusted” rates

19.4.1 Fit the model

# Hoffmann Example 6.5
glm_possion_2 <- glm(volteer ~ female + nonwhite + educate + income,
                     data = df_gss,
                     family = poisson(link = "log"))

summary(glm_possion_2)


Call:
glm(formula = volteer ~ female + nonwhite + educate + income, 
    family = poisson(link = "log"), data = df_gss)

Coefficients:
                  Estimate Std. Error z value Pr(>|z|)    
(Intercept)       -3.15830    0.24479 -12.902  < 2e-16 ***
femaleFemale       0.26132    0.07785   3.357 0.000789 ***
nonwhiteNon-White -0.28038    0.10838  -2.587 0.009681 ** 
educate            0.10280    0.01443   7.123 1.05e-12 ***
income             0.05683    0.01566   3.628 0.000286 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 2566.8  on 1943  degrees of freedom
Residual deviance: 2465.5  on 1939  degrees of freedom
  (959 observations deleted due to missingness)
AIC: 3380.9

Number of Fisher Scoring iterations: 6

19.4.2 Parameter Estimates

apaSupp::tab_glm(glm_possion_2,
                 var_labels = c(female = "Female vs Male",
                                nonwhite = "Nonwhite vs White",
                                educate = "Education",
                                income = "Income"),
                 show_single_row = c("female", "nonwhite"),
                 p_note = "apa23")

**Table 19.5**
Parameter Estimates for Generalized Linear Regression
	Incident Rate Ratio		Log Scale
Variable	IRR	95% CI	b	(SE)	Wald	LRT	VIF
(Intercept)	0.04	[0.03, 0.07]	-3.16	(0.24)	< .001***
Female vs Male	1.30	[1.12, 1.51]	0.26	(0.08)	< .001***	< .001***	1.05
Nonwhite vs White	0.76	[0.61, 0.93]	-0.28	(0.11)	.010**	.008**	1.01
Education	1.11	[1.08, 1.14]	0.10	(0.01)	< .001***	< .001***	1.07
Income	1.06	[1.03, 1.09]	0.06	(0.02)	< .001***	< .001***	1.11
pseudo-R²	.069
Note. N = 1944. CI = confidence interval; VIF = variance inflation factor. Significance denotes Wald t-tests for individual parameter estimates, as well as Likelihood Ratio Tests (LRT) for single-predictor deletion. Coefficient of determination displays Nagelkerke's pseudo-R².
p < .01. * p < .001.

Interpretation:

female: Adjusting for the effects of race, education, and income, FEMALES are expected to volunteer about 30% MORE activities per year than males, IRR = 1.29, p < .001.
nonwhite: Adjusting for the effects of sex, education, and income, NON-WHITES are expected to volunteer for about 24% LESS activities per year than males, IRR = 0.76, p = .001.
educate: Each one-year increase in education is associated with an 11% increase in the number of volunteer activities per year, adjusting for the effects of sex, race/ethnicity, and income, IRR = 1.11, p <.001.
income: Each additional $1000 a household makes is associated with a 6% increase in the number of times a person volunteers per year, controlling for sex, race, and education, IRR = 1.06, p < .001.

19.4.3 Predictions

Note: These means are on the original scale (number of volunteer activities in the past year). Stata calculates so-called “delta-method standard errors” , but they are not calculated here in R.

ggeffects::ggemmeans(model = glm_possion_2,
                     terms = c("female"),
                     condition = c(nonwhite = "White",
                                   educate = 12,
                                   income = 5))

# A tibble: 2 × 6
  x      predicted std.error conf.low conf.high group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <fct>
1 Male       0.194    0.109     0.157     0.240 1    
2 Female     0.252    0.0952    0.209     0.303 1

(0.25 - 0.19) / 0.19

[1] 0.3157895

0.25/0.19

[1] 1.315789

Interpretation:

The expected number of volunteer activities in a year among females is 31.5% higher than among males, for white high school graduates with low income.

Note: income = 5 is the 10th percentile of the income distribution.

19.4.4 Assess Model Fit

DescTools::PseudoR2(glm_possion_2)

  McFadden 
0.02918402

DescTools::PseudoR2(glm_possion_2, which = "all") %>% round(3)

       McFadden     McFaddenAdj        CoxSnell      Nagelkerke   AldrichNelson 
          0.029           0.026           0.051           0.061           0.050 
VeallZimmermann           Efron McKelveyZavoina            Tjur             AIC 
          0.077           0.020              NA              NA        3380.860 
            BIC          logLik         logLik0              G2 
       3408.722       -1685.430       -1736.096         101.333

Interpretation:

Although these four predictors (sex, race, education, and income) are associated with differences in the number of times a person volunteers annually, together they account for very little of the variance, $R^2_{McF} = .029$, $R^2_{Nag} = .061$.

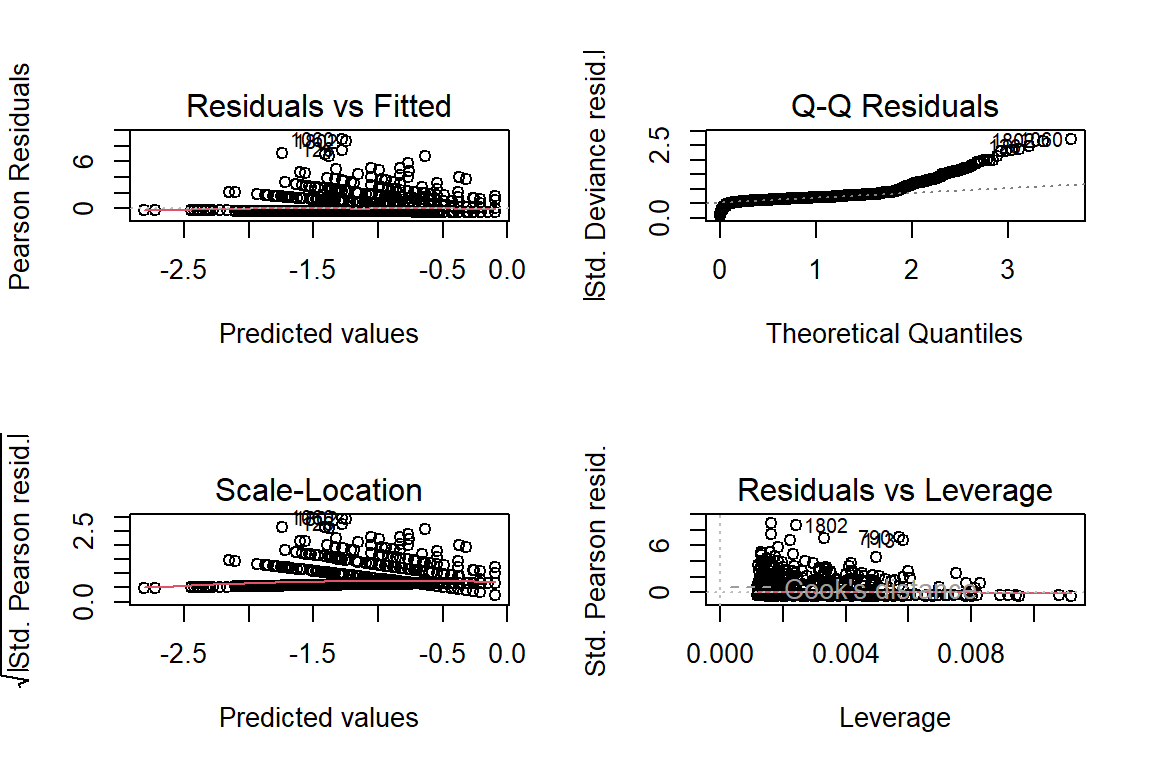
19.4.5 Residual Diagnostics

par(mfrow = c(2, 2))
plot(glm_possion_2)

par(mfrow = c(1, 1))

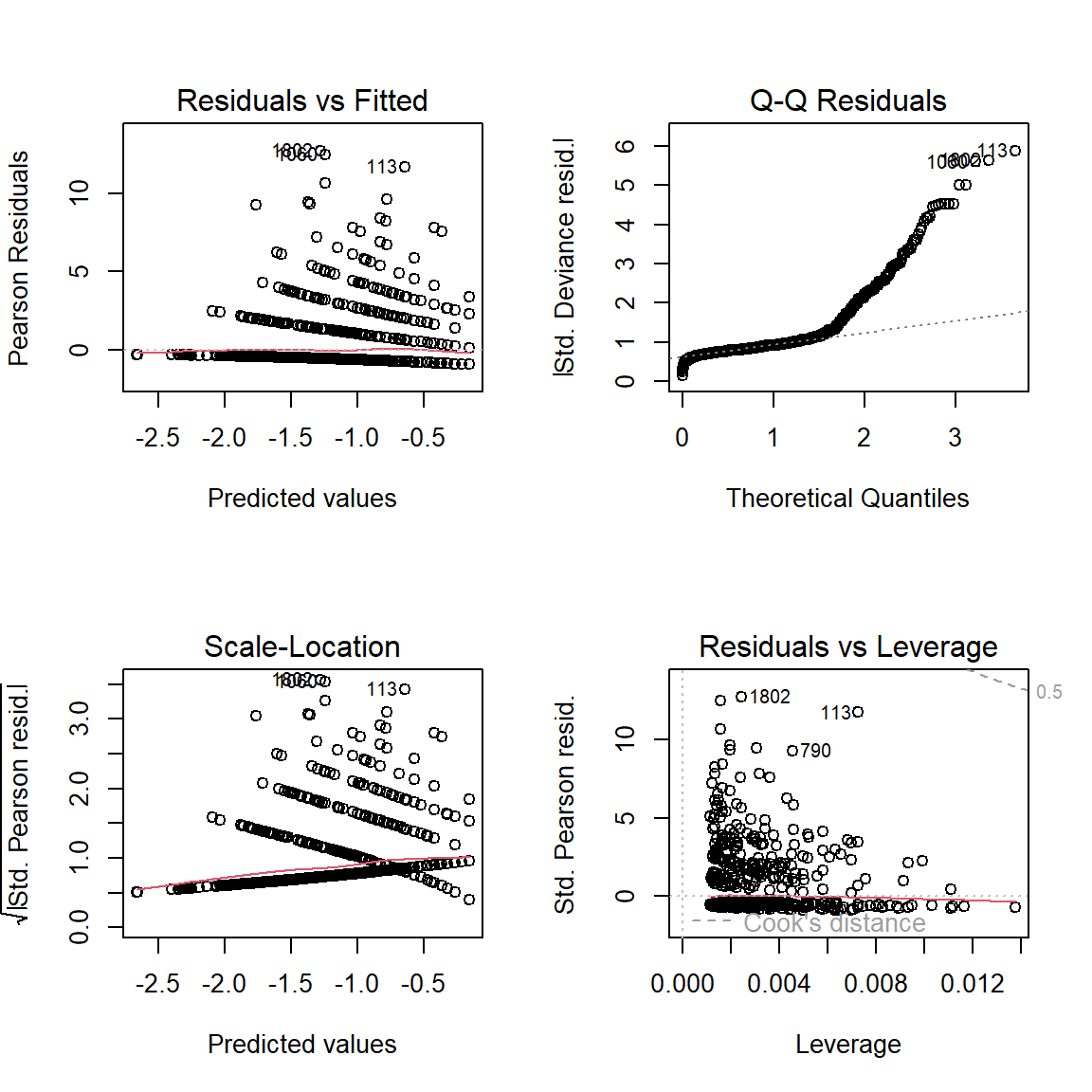
Interpretation:

These residuals do NOT look good, especially the Q-Q plot for normality.

19.4.6 Marginal Plot

df_gss %>% 
  dplyr::select(educate, income) %>% 
  apaSupp::tab_desc()

**Table 19.6**
Summary of Quantiatative Variables
	NA	M	SD	min	Q1	Mdn	Q3	max
educate	9	13.36	2.93	0.00	12.00	13.00	16.00	20.00
income	956	9.86	2.99	1.00	9.00	11.00	12.00	12.00
Note. N = 2903. NA = not available or missing; Mdn = median; Q1 = 25th percentile; Q3 = 75th percentile.

interactions::interact_plot(model = glm_possion_2,
                            pred = educate,
                            modx = female,
                            mod2 = nonwhite) +
  theme_bw()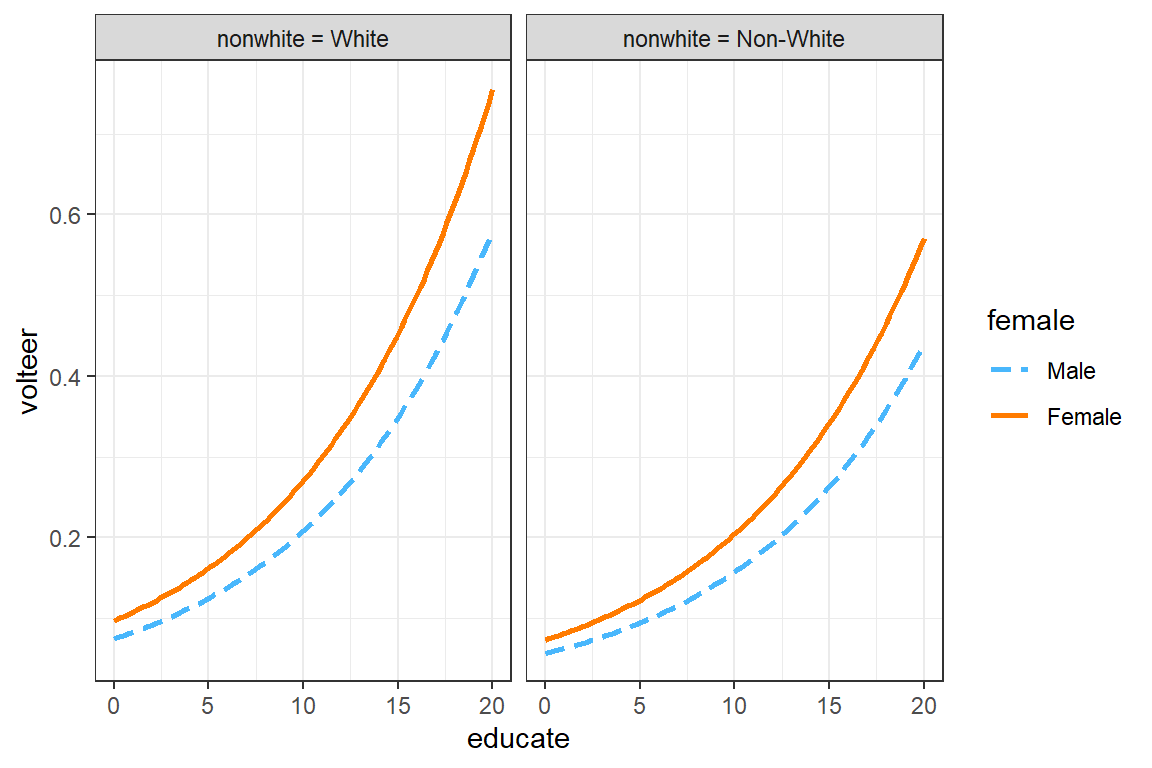

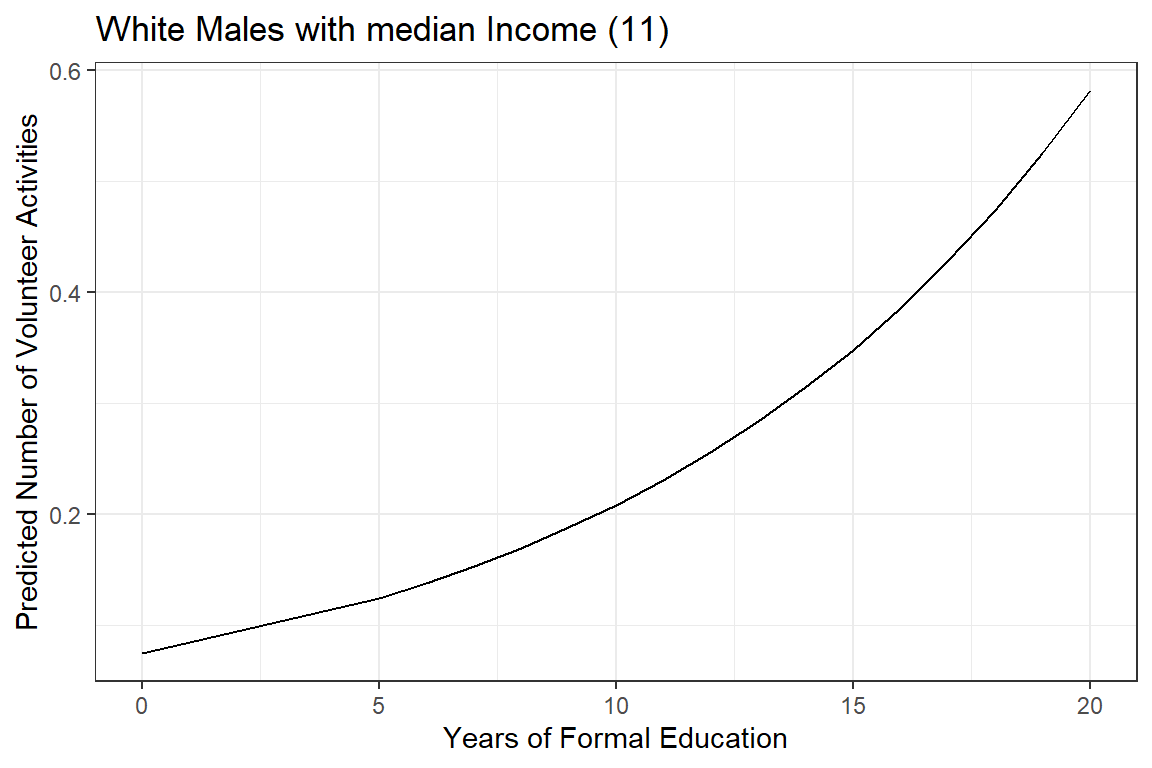
ggeffects::ggemmeans(model = glm_possion_2,
                     terms = "educate",
                     condition = c(female = "Male",
                                   nonwhite = "White",
                                   incomeN = 11)) %>% 
  data.frame %>% 
  ggplot(aes(x = x,
             y = predicted)) +
  geom_line() +
  theme_bw() +
  labs(x = "Years of Formal Education",
       y = "Predicted Number of Volunteer Activities",
       title = "White Males with median Income (11) ")

Figure 19.2
Hoffmann’s Figure 6.5

effects::Effect(focal.predictors = c("female", "nonwhite", "educate", "income"),
                mod = glm_possion_2,
                xlevels = list(educate = seq(from = 0, to = 20, by = .1),
                               income  = c(8, 10, 12))) %>% 
  data.frame() %>% 
  dplyr::mutate(income = factor(income) %>% 
                  forcats::fct_recode("Lower Income (8)" = "8",
                                      "Middle Income (10)" = "10",
                                      "Higher Income (12)" = "12")) %>% 
  ggplot(aes(x = educate,
             y = fit)) +
  geom_ribbon(aes(ymin = fit - se,  # bands = +/- 1 SEM
                  ymax = fit + se,
                  fill = female),
              alpha = .2) +
  geom_line(aes(linetype = female,
                color = female),
            size = 1) +
  theme_bw() +
  labs(x = "Education, Years",
       y = "Predicted Mean Number of Volunteer Activities",
       color = NULL,
       fill = NULL,
       linetype = NULL) +
  theme(legend.position = c(0, 1),
        legend.justification = c(-.1, 1.1),
        legend.background = element_rect(color = "black"),
        legend.key.width = unit(2, "cm")) +
  facet_grid(nonwhite ~ income)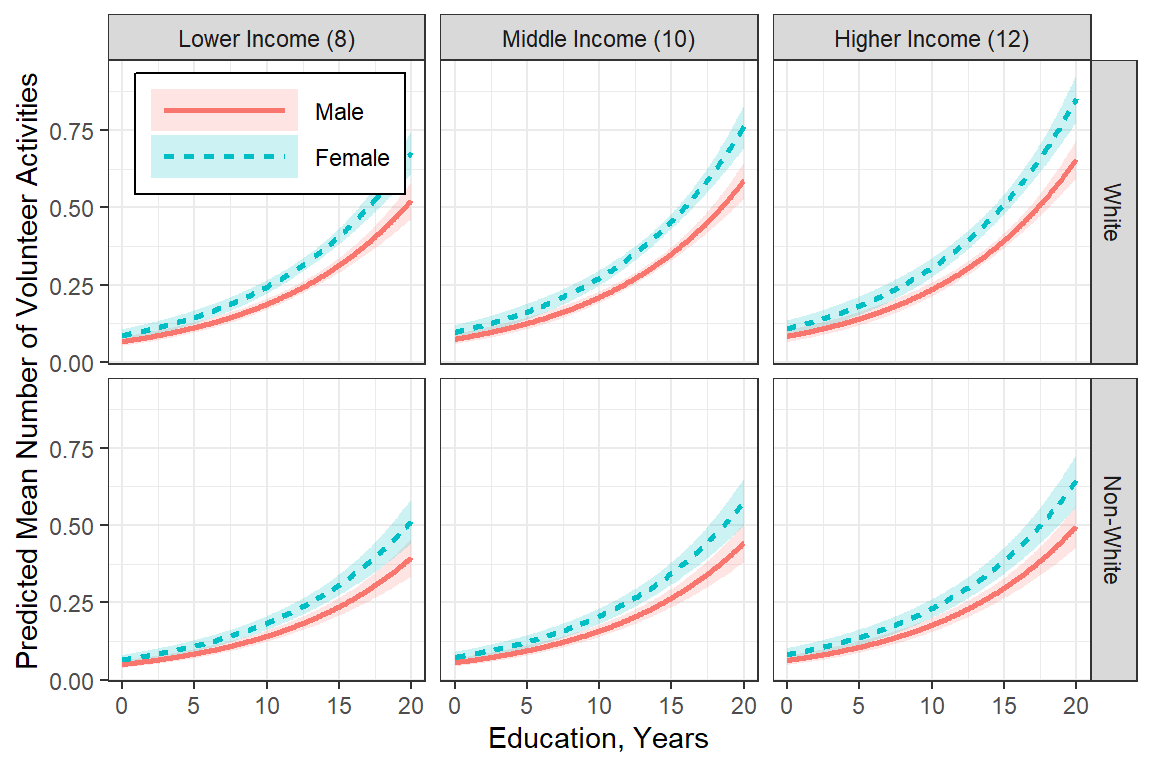

effects::Effect(focal.predictors = c("female", "nonwhite", "educate", "income"),
                mod = glm_possion_2,
                xlevels = list(educate = seq(from = 0, to = 20, by = .1),
                               income  = c(5, 8, 12))) %>% 
  data.frame() %>% 
  dplyr::mutate(income = factor(income)) %>% 
  ggplot(aes(x = educate,
             y = fit)) +
  geom_line(aes(linetype = fct_rev(income),
                color = fct_rev(income)),
            size = 1) +
  theme_bw() +
  labs(x = "Education, Years",
       y = "Predicted Mean Number of Volunteer Activities",
       color = "Income:",
       fill = "Income:",
       linetype = "Income:") +
  theme(legend.position = c(0, 1),
        legend.justification = c(-.1, 1.1),
        legend.background = element_rect(color = "black"),
        legend.key.width = unit(2, "cm")) +
  facet_grid(nonwhite ~ female) +
  scale_linetype_manual(values = c("solid", "longdash", "dotted"))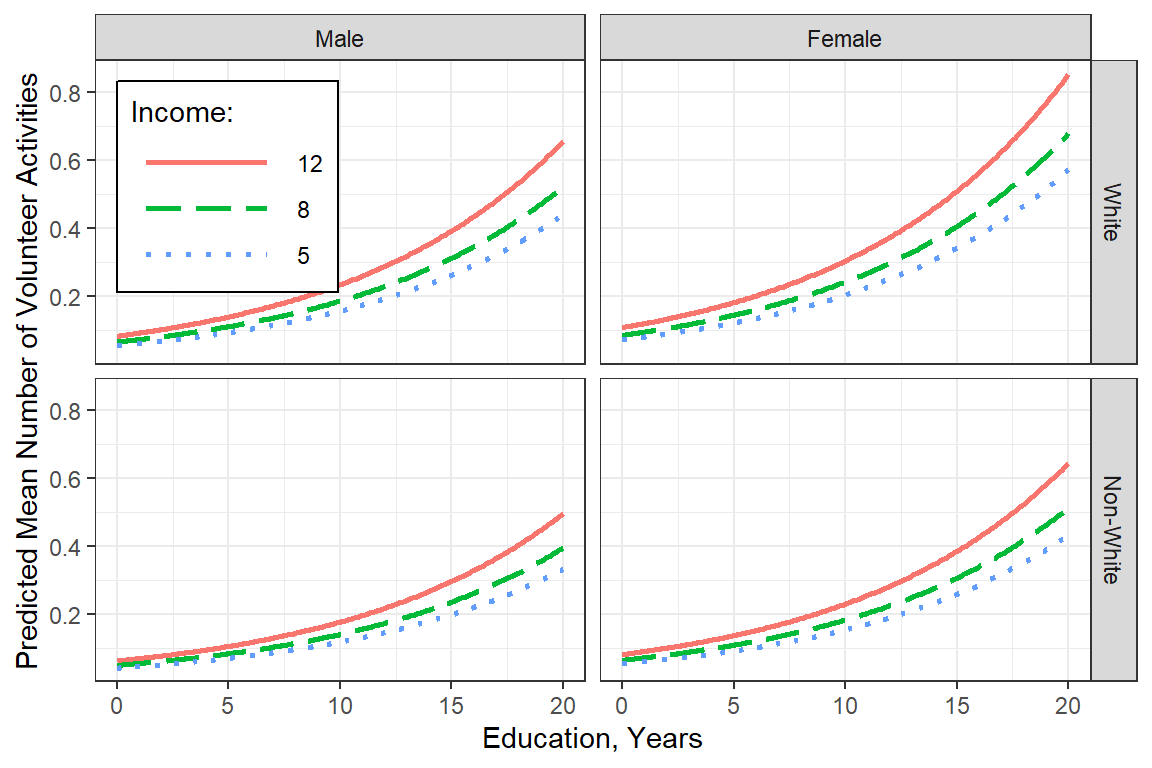

effects::Effect(focal.predictors = c("female", "nonwhite", "educate", "income"),
                mod = glm_possion_2,
                xlevels = list(educate = seq(from = 0, to = 20, by = .1),
                               income  = c(8, 10, 12))) %>% 
  data.frame() %>% 
  dplyr::mutate(income = factor(income) %>% 
                  forcats::fct_recode("Lower Income (8)" = "8",
                                      "Middle Income (10)" = "10",
                                      "Higher Income (12)" = "12")) %>% 
  ggplot(aes(x = educate,
             y = fit)) +
  geom_ribbon(aes(ymin = fit - se,  # bands = +/- 1 SEM
                  ymax = fit + se,
                  fill = nonwhite),
              alpha = .2) +
  geom_line(aes(linetype = nonwhite,
                color = nonwhite),
            size = 1) +
  theme_bw() +
  labs(x = "Education, Years",
       y = "Predicted Mean Number of Volunteer Activities",
       color = NULL,
       fill = NULL,
       linetype = NULL) +
  theme(legend.position = c(0, .5),
        legend.justification = c(-.05, 1.1),
        legend.background = element_rect(color = "black"),
        legend.key.width = unit(2, "cm")) +
  facet_grid(female ~ income) +
  scale_color_manual(values = c("darkgreen", "orange")) +
  scale_fill_manual(values = c("darkgreen", "orange"))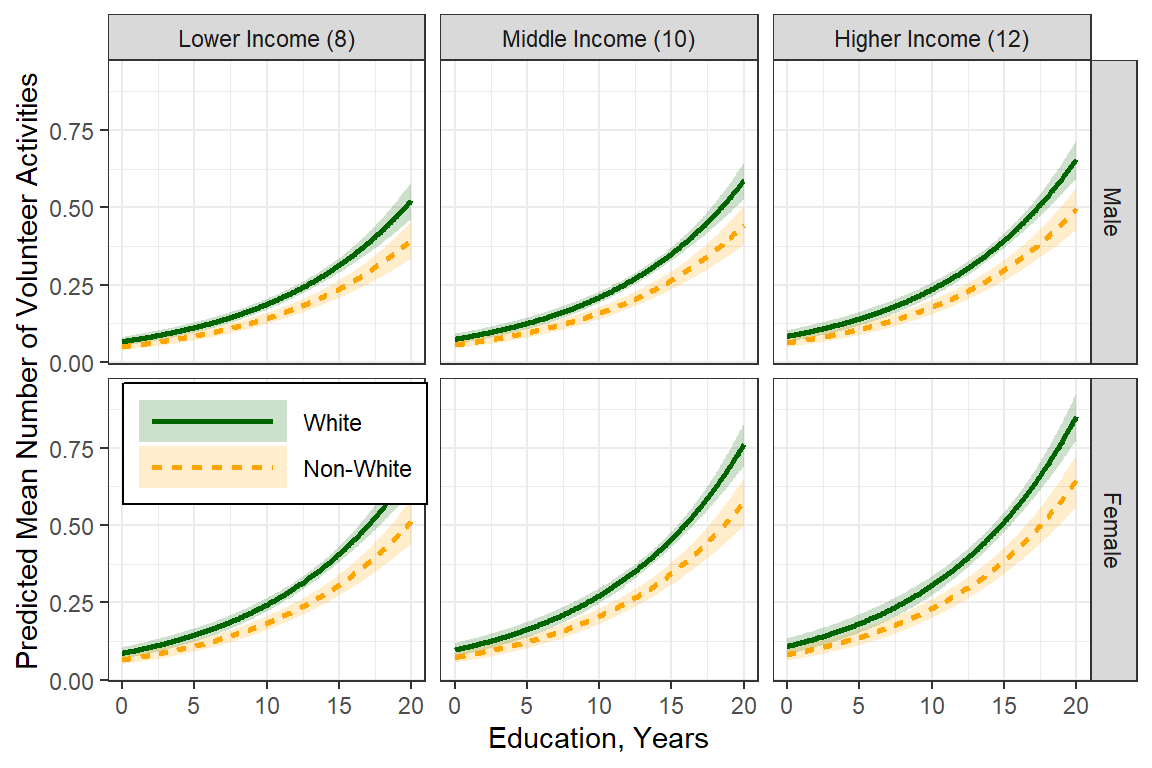

effects::Effect(focal.predictors = c("female", "educate"),
                mod = glm_possion_2,
                xlevels = list(educate = seq(from = 0,
                                             to   = 20,
                                             by = .1),
                               income = 11)) %>%          #Median Income
  data.frame() %>% 
  ggplot(aes(x = educate,
             y = fit,
             group = female)) +
  geom_ribbon(aes(ymin = fit - se,  # bands = +/- 1 SEM
                  ymax = fit + se),
              alpha = .2) +
  geom_line(aes(linetype = female),
            size = 1) +
  theme_bw() +
  labs(x = "Education, Years",
       y = "Predicted Mean Number of Volunteer Activities",
       color = NULL,
       fill = NULL,
       linetype = NULL) +
  theme(legend.position = c(0, 1),
        legend.justification = c(-.1, 1.1),
        legend.background = element_rect(color = "black"),
        legend.key.width = unit(2, "cm")) +
  scale_linetype_manual(values = c("solid", "longdash"))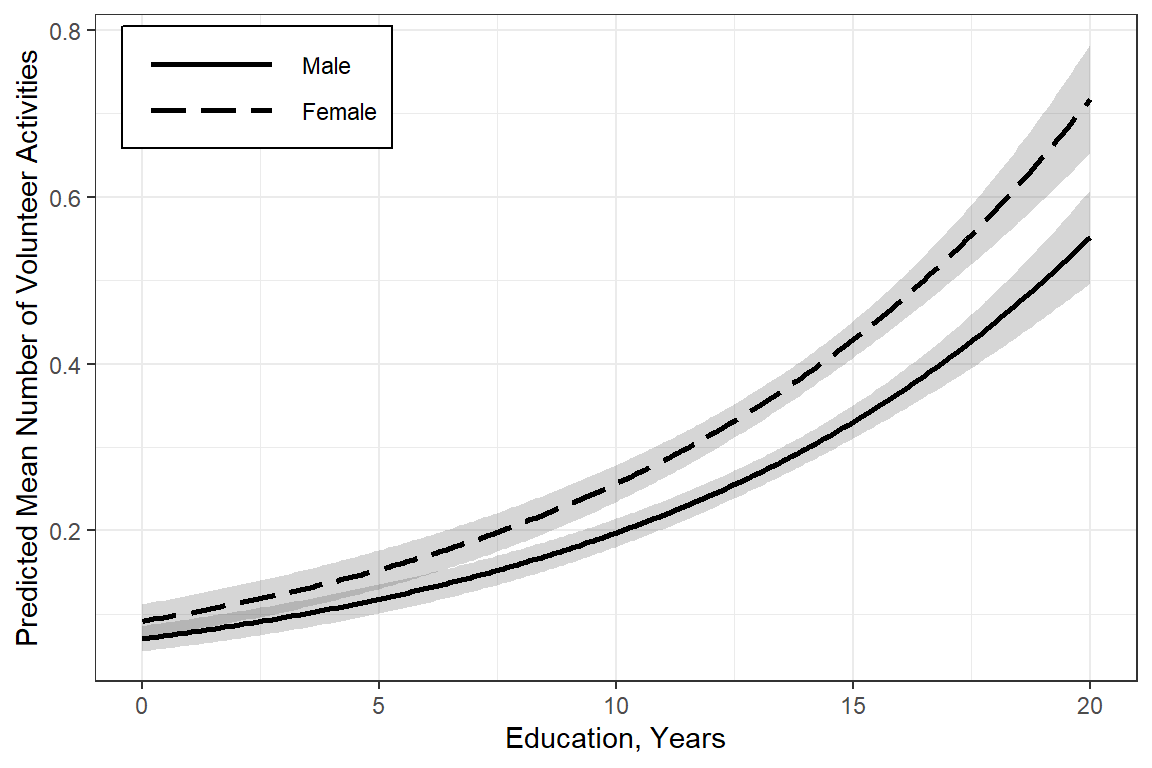

19.5 NEGATIVE BINOMIAL REGRESSION

19.5.1 Multiple Predictors

19.5.1.1 Fit the model

glm_negbin_1 <- MASS::glm.nb(volteer ~ female + nonwhite + educate + income,
                             data = df_gss)

summary(glm_negbin_1)


Call:
MASS::glm.nb(formula = volteer ~ female + nonwhite + educate + 
    income, data = df_gss, init.theta = 0.2559648877, link = log)

Coefficients:
                  Estimate Std. Error z value Pr(>|z|)    
(Intercept)       -3.24738    0.37283  -8.710  < 2e-16 ***
femaleFemale       0.28441    0.12312   2.310   0.0209 *  
nonwhiteNon-White -0.31107    0.16203  -1.920   0.0549 .  
educate            0.11200    0.02321   4.825  1.4e-06 ***
income             0.05193    0.02264   2.293   0.0218 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Negative Binomial(0.256) family taken to be 1)

    Null deviance: 1068.5  on 1943  degrees of freedom
Residual deviance: 1024.3  on 1939  degrees of freedom
  (959 observations deleted due to missingness)
AIC: 2851.6

Number of Fisher Scoring iterations: 1

              Theta:  0.2560 
          Std. Err.:  0.0251 

 2 x log-likelihood:  -2839.5640

Note: the deviance residuals all have absolute values less than 3-4’ish…better than before

Theta in R = 1/alpha in Stata

# Hoffmann Example 6.5
texreg::knitreg(list(glm_possion_2, 
                       texreghelpr::extract_glm_exp(glm_possion_2,
                                                    include.aic = FALSE,
                                                    include.bic = FALSE,
                                                    include.loglik = FALSE,
                                                    include.deviance = FALSE,
                                                    include.nobs = FALSE)),
                  custom.model.names = c("b (SE)", "IRR [95% CI]"),
                  custom.coef.map = list("(Intercept)" ="Intercept",
                                         femalefemale = "Female vs. Male",
                                         "nonwhitenon-white" = "Non-white vs. White",
                                         educate = "Education, years",
                                         income = "Income, 1000's"),
                  caption = "GLM: Multiple Possion Regression",
                  single.row = TRUE,
                  digits = 3)

GLM: Multiple Possion Regression
	b (SE)	IRR [95% CI]
Intercept	-3.158 (0.245)^***	0.042 [0.026; 0.068]^*
Education, years	0.103 (0.014)^***	1.108 [1.077; 1.140]^*
Income, 1000’s	0.057 (0.016)^***	1.058 [1.027; 1.092]^*
AIC	3380.860
BIC	3408.722
Log Likelihood	-1685.430
Deviance	2465.514
Num. obs.	1944
^*p < 0.001; ^p < 0.01; ^*p < 0.05 (or Null hypothesis value outside the confidence interval).

19.5.1.2 Predictions

Note: These means are on the original scale (number of volunteer activities in the past year). These standard errors are called “delta-method standard errors”

effects::Effect(focal.predictors = c("female"),
                mod = glm_negbin_1,
                xlevels = list(nonwhite = "non-white",
                               educate = 5,
                               income = 12)) %>% 
  data.frame()

# A tibble: 2 × 5
  female   fit     se lower upper
  <fct>  <dbl>  <dbl> <dbl> <dbl>
1 Male   0.289 0.0257 0.243 0.344
2 Female 0.384 0.0322 0.326 0.453

ggeffects::ggemmeans(model = glm_negbin_1,
                     terms = c("female"),
                     condition = c(nonwhite = "White",
                                   educate = 12,
                                   income = 5))

# A tibble: 2 × 6
  x      predicted std.error conf.low conf.high group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <fct>
1 Male       0.193     0.157    0.142     0.263 1    
2 Female     0.257     0.137    0.196     0.336 1

Compare to the Poisson:

ggeffects::ggemmeans(model = glm_possion_2,
                     terms = c("female"),
                     condition = c(nonwhite = "White",
                                   educate = 12,
                                   income = 5))

# A tibble: 2 × 6
  x      predicted std.error conf.low conf.high group
  <fct>      <dbl>     <dbl>    <dbl>     <dbl> <fct>
1 Male       0.194    0.109     0.157     0.240 1    
2 Female     0.252    0.0952    0.209     0.303 1

Note: The predictions are very similar for Poisson and Negative Binomial…therefor the overdisperssion does not affect the sex difference much, but it may affect other things…

19.5.1.3 Parameter Estimates

Coefficients are in terms of the LOG of the number of times a person volunteers per year.

glm_negbin_1 %>% coef()

      (Intercept)      femaleFemale nonwhiteNon-White           educate 
      -3.24738340        0.28440826       -0.31107286        0.11199528 
           income 
       0.05193102

Exponentiating the coefficients (betas) returns the values to the original scale (number of times a person volunteers per year) and is called the incident rate ratio IRR.

glm_negbin_1 %>% coef() %>% exp()

      (Intercept)      femaleFemale nonwhiteNon-White           educate 
        0.0388758         1.3289754         0.7326605         1.1185076 
           income 
        1.0533031

texreg::knitreg(list(glm_negbin_1, 
                       texreghelpr::extract_glm_exp(glm_negbin_1,
                                                    include.aic = FALSE,
                                                    include.bic = FALSE,
                                                    include.loglik = FALSE,
                                                    include.deviance = FALSE,
                                                    include.nobs = FALSE)),
                  custom.model.names = c("b (SE)", "IRR [95% CI]"),
                  custom.coef.map = list("(Intercept)" ="Intercept",
                                         femaleFemale = "Female vs. Male",
                                         "nonwhitenon-white" = "Non-white vs. White",
                                         educate = "Education, Years",
                                         income = "Income"),
                  caption = "GLM: Negitive Binomial Regression",
                  single.row = TRUE,
                  digits = 3)

GLM: Negitive Binomial Regression
	b (SE)	IRR [95% CI]
Intercept	-3.247 (0.373)^***	0.039 [0.018; 0.081]^*
Female vs. Male	0.284 (0.123)^*	1.329 [1.043; 1.696]^*
Education, Years	0.112 (0.023)^***	1.119 [1.067; 1.173]^*
Income	0.052 (0.023)^*	1.053 [1.008; 1.101]^*
AIC	2851.564
BIC	2884.999
Log Likelihood	-1419.782
Deviance	1024.343
Num. obs.	1944
^*p < 0.001; ^p < 0.01; ^*p < 0.05 (or Null hypothesis value outside the confidence interval).

19.5.1.4 Residual Diagnostics

par(mfrow = c(2, 2))
plot(glm_negbin_1)

par(mfrow = c(1, 1))

These still don’t look very good :(

19.5.1.5 Compare models

performance::compare_performance(glm_possion_2, glm_negbin_1, rank = TRUE)

# A tibble: 2 × 11
  Name       Model R2_Nagelkerke  RMSE Sigma Score_log Score_spherical    AIC_wt
  <chr>      <chr>         <dbl> <dbl> <dbl>     <dbl>           <dbl>     <dbl>
1 glm_negbi… negb…        0.0531 0.919     1    -0.808          0.0210 1   e+  0
2 glm_possi… glm          0.0693 0.918     1    -0.867          0.0210 1.16e-115
# ℹ 3 more variables: AICc_wt <dbl>, BIC_wt <dbl>, Performance_Score <dbl>

19.6 ZIP: ZERO-INFLATED POISSON REGRESSION

19.6.1 Fit the model

glm_zip_1 <- pscl::zeroinfl(volteer ~ female + nonwhite + educate + income | educate,
                               data = df_gss)

summary(glm_zip_1)


Call:
pscl::zeroinfl(formula = volteer ~ female + nonwhite + educate + income | 
    educate, data = df_gss)

Pearson residuals:
    Min      1Q  Median      3Q     Max 
-0.5778 -0.4416 -0.3908 -0.3383  9.4777 

Count model coefficients (poisson with log link):
                  Estimate Std. Error z value Pr(>|z|)   
(Intercept)       -1.09660    0.34808  -3.150  0.00163 **
femaleFemale       0.20615    0.09452   2.181  0.02918 * 
nonwhiteNon-White -0.20101    0.13444  -1.495  0.13488   
educate            0.05648    0.02140   2.639  0.00833 **
income             0.04888    0.01882   2.597  0.00940 **

Zero-inflation model coefficients (binomial with logit link):
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  2.01161    0.41192   4.883 1.04e-06 ***
educate     -0.07179    0.02768  -2.593  0.00951 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 

Number of iterations in BFGS optimization: 18 
Log-likelihood: -1434 on 7 Df

glm_zip_1 %>% coef() %>% exp()

      count_(Intercept)      count_femaleFemale count_nonwhiteNon-White 
              0.3340048               1.2289390               0.8179079 
          count_educate            count_income        zero_(Intercept) 
              1.0581037               1.0500947               7.4753687 
           zero_educate 
              0.9307240

Compares two models fit to the same data that do not nest via Vuong’s non-nested test.

pscl::vuong(glm_zip_1, glm_possion_2)

Vuong Non-Nested Hypothesis Test-Statistic: 
(test-statistic is asymptotically distributed N(0,1) under the
 null that the models are indistinguishible)
-------------------------------------------------------------
              Vuong z-statistic             H_A    p-value
Raw                    8.000302 model1 > model2 6.6613e-16
AIC-corrected          7.936568 model1 > model2 9.9920e-16
BIC-corrected          7.758989 model1 > model2 4.3299e-15

19.7 ZINB: ZERO-INFLATED NEGATIVE BINOMIAL

19.7.1 Fit the model

glm_zinb_1 <- pscl::zeroinfl(volteer ~ female + nonwhite + educate + income | educate,
                               data = df_gss,
                             dist = "negbin")

summary(glm_zinb_1)


Call:
pscl::zeroinfl(formula = volteer ~ female + nonwhite + educate + income | 
    educate, data = df_gss, dist = "negbin")

Pearson residuals:
    Min      1Q  Median      3Q     Max 
-0.5146 -0.4122 -0.3704 -0.3222  8.8088 

Count model coefficients (negbin with log link):
                  Estimate Std. Error z value Pr(>|z|)   
(Intercept)       -1.79278    0.54745  -3.275  0.00106 **
femaleFemale       0.26245    0.11745   2.235  0.02545 * 
nonwhiteNon-White -0.28519    0.15603  -1.828  0.06758 . 
educate            0.06817    0.03317   2.055  0.03987 * 
income             0.05292    0.02159   2.451  0.01426 * 
Log(theta)         0.05056    0.46242   0.109  0.91293   

Zero-inflation model coefficients (binomial with logit link):
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)  1.28322    0.71435   1.796   0.0724 .
educate     -0.07208    0.04684  -1.539   0.1238  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 

Theta = 1.0519 
Number of iterations in BFGS optimization: 33 
Log-likelihood: -1416 on 8 Df

glm_zinb_1 %>% coef() %>% exp()

      count_(Intercept)      count_femaleFemale count_nonwhiteNon-White 
              0.1664962               1.3001110               0.7518708 
          count_educate            count_income        zero_(Intercept) 
              1.0705424               1.0543416               3.6082563 
           zero_educate 
              0.9304550

19.8 Compare Models

pscl::vuong(glm_zinb_1, glm_negbin_1)

Vuong Non-Nested Hypothesis Test-Statistic: 
(test-statistic is asymptotically distributed N(0,1) under the
 null that the models are indistinguishible)
-------------------------------------------------------------
              Vuong z-statistic             H_A  p-value
Raw                   1.3486325 model1 > model2 0.088728
AIC-corrected         0.5592035 model1 > model2 0.288011
BIC-corrected        -1.6403440 model2 > model1 0.050467

pscl::vuong(glm_zip_1, glm_zinb_1)

Vuong Non-Nested Hypothesis Test-Statistic: 
(test-statistic is asymptotically distributed N(0,1) under the
 null that the models are indistinguishible)
-------------------------------------------------------------
              Vuong z-statistic             H_A   p-value
Raw                   -2.428612 model2 > model1 0.0075784
AIC-corrected         -2.428612 model2 > model1 0.0075784
BIC-corrected         -2.428612 model2 > model1 0.0075784

performance::compare_performance(glm_possion_2, glm_zip_1, 
                                 glm_negbin_1, glm_zinb_1) %>% 
  data.frame() %>% 
  dplyr::select(Name, AICc, BIC, RMSE,
                R2, R2_adjusted, R2_Nagelkerke) %>% 
  dplyr::mutate(across(starts_with("R2"), ~apaSupp::p_num(.x, stars = FALSE))) %>% 
  flextable::flextable() %>% 
  apaSupp::theme_apa(caption = "Compare Model Fits")

**Table 19.7**
Compare Model Fits
Name	AICc	BIC	RMSE	R2	R2_adjusted	R2_Nagelkerke
glm_possion_2	3,380.89	3,408.72	0.92			.069
glm_zip_1	2,882.81	2,921.76	0.92	.016	.013
glm_negbin_1	2,851.61	2,885.00	0.92			.053
glm_zinb_1	2,848.80	2,893.31	0.92	.020	.018

The ‘best’ model is the zero-inflated negative binomial

## Final

glm_possion_2 %>% 
  emmeans::emmeans(~ female + educate + income,
                   at = list(educate = seq(from = 8,
                                             to = 18,
                                             by = .1),
                               income  = c(8, 10, 12)),
                   type = "response") %>% 
  data.frame() %>% 
  dplyr::mutate(income = factor(income) %>% 
                  forcats::fct_recode("Lower Income (8)" = "8",
                                      "Middle Income (10)" = "10",
                                      "Higher Income (12)" = "12")) %>% 
  dplyr::mutate(income = forcats::fct_rev(income)) %>% 
  dplyr::mutate(female = forcats::fct_rev(female)) %>% 
  ggplot(aes(x = educate,
             y = rate)) +
  geom_vline(xintercept = 12) +
  geom_line(aes(linetype = income,
                color = female),
            size = 1) +
  theme_bw() +
  labs(x = "Education, Years",
       y = "Predicted Rate\nVolunteer Activities in the Prior Year",
       color = NULL,
       fill = NULL,
       linetype = NULL) +
  theme(legend.position = c(0, 1),
        legend.justification = c(-.1, 1.1),
        legend.background = element_rect(color = "black"),
        legend.key.width = unit(2, "cm")) +
  scale_linetype_manual(values = c("solid", "longdash", "dotted")) +
  scale_x_continuous(breaks = seq(from = 8, to = 20, by = 2))

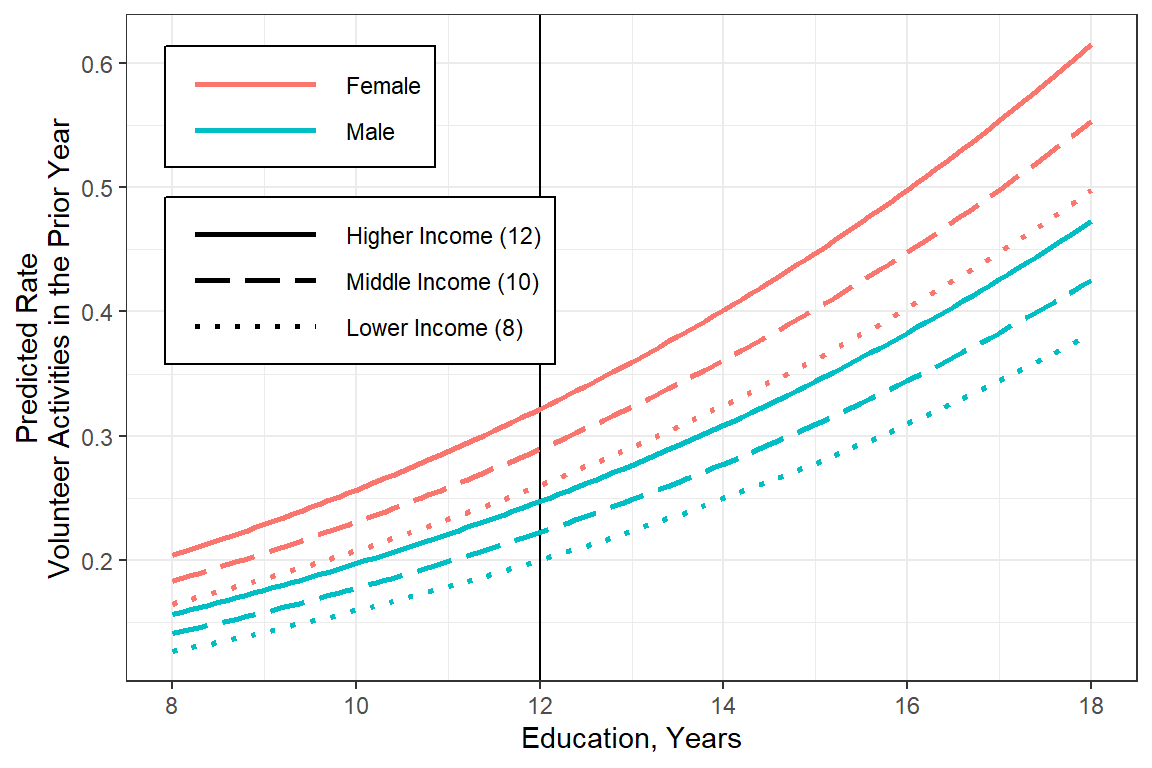
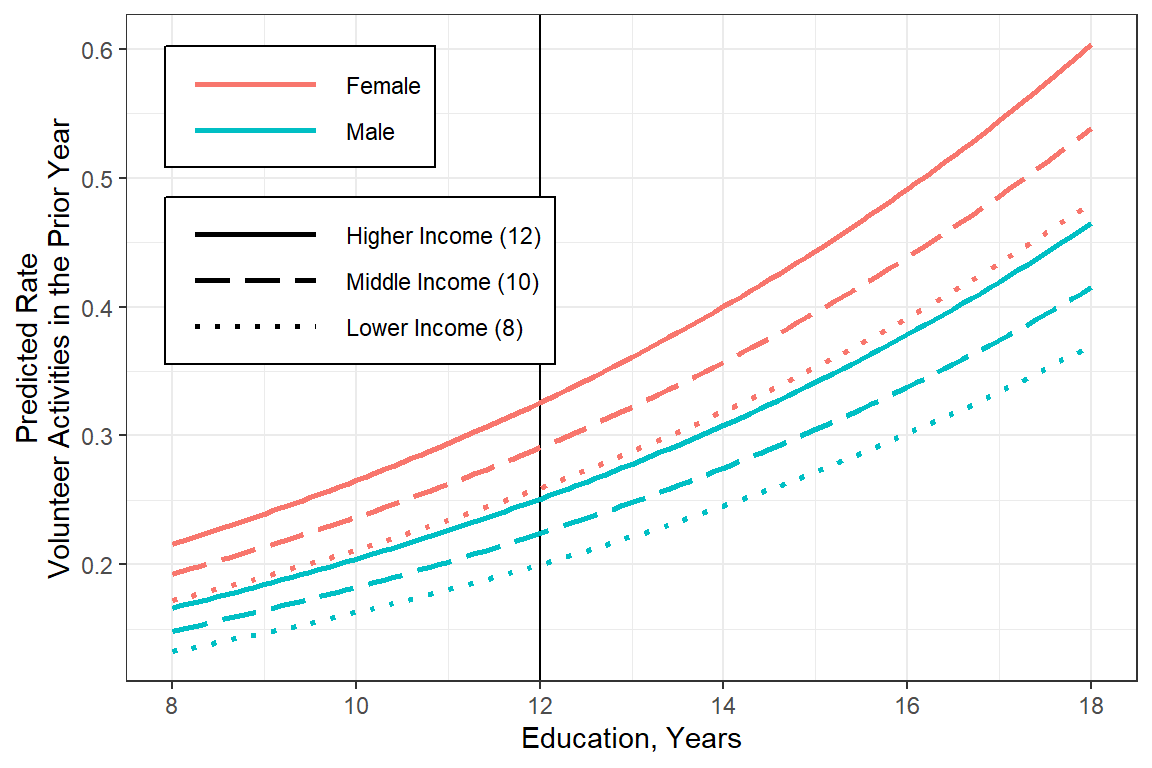
Figure 19.3
Worst Model: Poisson

glm_zinb_1 %>% 
  emmeans::emmeans(~ female + educate + income,
                   at = list(educate = seq(from = 8,
                                             to = 18,
                                             by = .1),
                               income  = c(8, 10, 12)),
                   type = "response") %>% 
  data.frame() %>% 
  dplyr::mutate(income = factor(income) %>% 
                  forcats::fct_recode("Lower Income (8)" = "8",
                                      "Middle Income (10)" = "10",
                                      "Higher Income (12)" = "12")) %>% 
  dplyr::mutate(income = forcats::fct_rev(income)) %>% 
  dplyr::mutate(female = forcats::fct_rev(female)) %>% 
  ggplot(aes(x = educate,
             y = emmean)) +
  geom_vline(xintercept = 12) +
  geom_line(aes(linetype = income,
                color = female),
            size = 1) +
  theme_bw() +
  labs(x = "Education, Years",
       y = "Predicted Rate\nVolunteer Activities in the Prior Year",
       color = NULL,
       fill = NULL,
       linetype = NULL) +
  theme(legend.position = c(0, 1),
        legend.justification = c(-.1, 1.1),
        legend.background = element_rect(color = "black"),
        legend.key.width = unit(2, "cm")) +
  scale_linetype_manual(values = c("solid", "longdash", "dotted")) +
  scale_x_continuous(breaks = seq(from = 8, to = 20, by = 2))

Figure 19.4
Best Model: Zero Inflated Negative Binomial